曲轴工艺尺寸链出错分析及避免方法
问题背景
我司某型发动机曲轴上法兰侧端面至法兰轴颈端面之间的距离尺寸——“凸台”高度(“凸台”结构如图1所示)在加工中有时会超差,呈现一定的不规律性,即连续加工的工件一段时间尺寸合格一段时间尺寸不合格,由于该尺寸为间接形成的尺寸,控制该尺寸的工序(精磨法兰轴颈及端面)只是监视其是否合格,而不能独立通过调整使其合格,因此需要通过尺寸链计算来分析其影响因素。但是该尺寸形成过程较复杂,尺寸链涉及尺寸较多,尺寸间关系较复杂,计算时经常出错,对问题的分析和解决造成了较大困难。
为了解决该问题,我司对该尺寸的尺寸链的计算过程进行了深入分析,并找到了计算错误的原因,最终找到了该尺寸的真正影响因素,进而通过调整或控制对其有影响的尺寸,显著提高了该尺寸的合格率。

尺寸链分析
1.“凸台”高度的形成过程及工艺尺寸链图
“凸台”高度是一个粗加工面与精加工面的间距尺寸,其形成过程与四道工序有关,具体为平头打孔(图2)、精车(图3)、滚压(图4)及精磨(图5)。
将“凸台”高度的形成过程,汇总在一张图上(类似尺寸链跟踪图),尺寸A、B、C、D、E、G如图6所示。
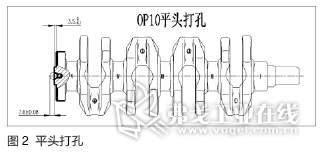
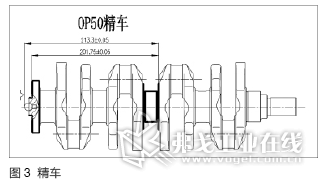
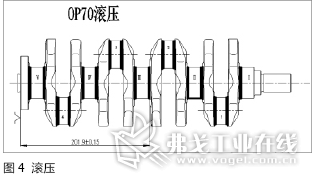
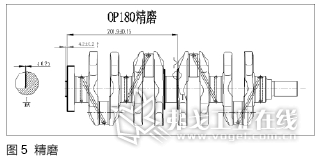
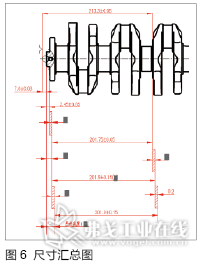
2.尺寸链计算过程
(1)计算方法1
1)步骤1:尺寸7.6、(3.45±0.05)、213.3、201.75与B构成尺寸链,B=(213.3±0.05)-(7.6±0.08)-(3.45±0.05)-(201.75±0.05)=0.5±0.23。
2)步骤2:尺寸(201.9±0.15(E))、0.2、(201.9±0.15)与C构成尺寸链,C=(201.9±0.15(E))+0.2-(201.9±0.15)=0.2±0.3。
3)步骤3:尺寸A与B、C、(3.45±0.05)构成尺寸链,A=(3.45±0.05)+B+C=(3.45±0.05)+(0.5±0.23)+(0.2±0.3)=4.15±0.58。
(2)计算方法2
1)步骤1:尺寸(213.3±0.05)、(7.6±0.08)、D、(201.75±0.05)构成尺寸链,D=(213.3±0.05)-(7.6±0.08)-(201.75±0.05)=3.95±0.18。
2)步骤2:尺寸D、(201.9±0.15(E))、0.2、(201.9±0.15)、A构成尺寸链,A=D+(201.9±0.15)+0.2-(201.9±0.15)=(3.95±0.18)+(201.9±0.15)+0.2-(201.9±0.15)=4.15±0.48。
计算方法1与计算方法2的计算结果不一致,说明至少有一种方法的结果是错误的。
错误分析
经分析发现方法1的计算是错误的,原因为尺寸B与尺寸(3.45±0.05)有关系,尺寸B会受尺寸(3.45±0.05)的影响,即尺寸B和尺寸(3.45±0.05)的公差不能同时达到极限尺寸。例如,当(3.45±0.05)尺寸为最大值3.5时,尺寸B的公差则会变为(0.45±0.18),达不到(0.5±0.23)。
两个尺寸在尺寸链中的方向相同,只有两个尺寸同时达到上极限偏差或下极限偏差,封闭环(尺寸A)才能达到极限值,如果两个尺寸不能同时达到极限尺寸,则封闭环(尺寸A)也不能达到计算结果的极限尺寸,因此方法1的计算结果是错误的。
方法2的计算过程也是错误的,因为尺寸(201.9±0.15(E))不是“独立”的尺寸,该尺寸为滚压后长度,表面上看是一个“自主”的尺寸,但该尺寸实际上受滚压前长度尺寸(201.75±0.05)的影响,即不存在(201.75±0.05)达到下极限偏差而(201.9±0.15(E))达到上极限偏差的情况。即如果滚压前长度尺寸(201.75±0.05)为下极限尺寸201.7时,则滚压后长度尺寸(201.9±0.15(E))不会达到上极限尺寸202.05。
而两个尺寸在方法2尺寸链中的方向相反,只有一个达到上差另一个达到下极限偏差,封闭环才能达到极限尺寸,如果两个尺寸不能同时达到极限尺寸,则封闭环也不能达到计算结果的极限尺寸,因此方法2的计算结果是错误的。
综上,两种尺寸链计算方法之所以出现错误,都是因为组成环中含有“不独立”的尺寸,其尺寸值受其他尺寸的实际值影响,该尺寸是否能够达到极限值和与其有关系的尺寸的实际值有关,因此,直接使用该尺寸的极限值计算出来的封闭环的公差是错误的。
解决方法
解决办法就是将组成环中“不独立”的尺寸拆分成“独立”的尺寸。以计算方法2为基础进行改进,该尺寸链组成环中只有滚压后长度(201.9±0.15(E))是“不独立”的尺寸,该尺寸可以拆分成滚压前长度(201.75±0.05)和滚压伸长量G(0.15±0.1)两个“独立”的尺寸。由于尺寸D也是由多个尺寸作用后形成的,因此也是不独立的尺寸,也需进行拆分。
拆分后,尺寸(7.6±0.08)、(213.3±0.05)、(0.15±0.1(G))、0.2、(201.9±0.15)和A组成尺寸链,A=-(7.6±0.08)+(213.3±0.05)+(0.15±0.1)+0.2-(201.9±0.15)=4.15±0.38。
结论
工艺尺寸链计算错误的唯一原因就是将不独立的尺寸作为尺寸链的组成环了。解决的办法就是找到组成环中不独立的尺寸,然后将不独立的尺寸拆分成独立的尺寸,最终让所有组成环尺寸都是独立的尺寸(不受其他尺寸影响的尺寸),然后再根据这些独立的尺寸所形成的尺寸链进行尺寸链计算。















跟帖
查看更多跟帖 已显示全部跟帖