0  前言

万向节的作用是在不同轴线上的轴之间进行转矩传递，所能传递转矩的大小受到材料性能、万向节结构和尺寸的限制。而在评价万向节性能时，万向节的承载能力和耐久磨损是评价万向节性能的重要指标^[1]。为了提升万向节的承载能力和寿命，部分学者针对万向节球道内部各部件之间的载荷、运动和接触应力进行了相关研究 ^[2-8]。通过 Hertz 理论能快速有效地计算球笼式万向节内部钢球与内外滚道之间的接触应力 ^[1,9]，但 Hertz 理论只能计算无摩擦和小变形条件下的接触应力 ^[10]，为了考虑摩擦或大变形条件等因素，部分学者采用有限元法计算万向节内部滚道的接触应力 ^[5-8]。陈静等 ^[6] 应用 ANSYS 软件对万向节内部钢球和内外滚道上的接触应力进行了分析，为了简化模型，将保持架与 6 个钢球固结在一起，这种简化对球道内部各个部件之间力的传递有影响，同时对整个万向节进行分析，由于网格误差和计算误差会引起部分滚道之间的接触应力差异较大，与实际结果存在差异。为了改善上述情况，本文对球笼式万向节的有限元模型进行改进，采用周期对称模型，按照球笼式万向节的工作原理和力的传递路径建立有限元模型，更符合实际。

1  球笼式万向节有限元模型

1.1 球笼式万向节模型简化

球笼式万向节内部结构复杂，零部件的结构特征较多，本文旨在研究球笼式万向节钢球和内外滚道之间的接触应力，故对整个模型进行适当的简化，将钟形壳外表面的花键、小倒角和圆角等不影响球道内部接触应力的特征进行简化。同时本文旨在研究球笼式万向节在无摆角状态下的接触应力，考虑到球笼式万向节在无摆角状态下满足周期对称条件，故本文对 6 球道球笼式万向节进行分割，取 1/6 模型进行分析计算，降低模型的计算规模，缩短计算时间的同时也降低模型收敛的难度。

1.2 球笼式万向节模型网格划分

球笼式万向节钢球与内外滚道内之间的接触属于Hertz 接触，接触区域的面积相对整个模型非常小，而应力却高度集中在靠近接触面的区域，并且在万向节运行过程中，球道内部的变形在微米级别，为了准确计算钢球与内外滚道之间的接触应力，需要对球道接触位置区域数模和网格进行精确划分，故本文采用二阶六面体网格，单元类型为 C3D10M，同时对球道内部钢球与内外滚道可能接触的区域网格进行细化以提高 Hertz 接触计算精度，而保持架与钟形壳和星型套之间的接触面积较大，且保持架模型规则，故本文采用六面体网格进行划分，单元类型为 C3D8。球笼式万向节各零部件网格划分如图1 ～ 4 所示。

图 1 钟形壳网格模型

图 2 星型套网格模型

图 3 钢球网格模型

图 4 保持架网格模型

1.3 球笼式万向节边界条件和接触设置

本文所述的万向节为 AC1500 系列，钢球的直径为 15.0813 mm。本文旨在研究万向节滚道内部接触应力随着加载转矩的变化，考虑到在实际路试过程中，AC1500 系列万向节所受的最大转矩小于或等于1000 N · m，故本文所加载的转矩为 1000 N · m，因本文采用周期对称约束，故加载的载荷为 166.67 N·m。如图 5 所示，在无摆角状态下，根据球笼万向节的结构特点，在传递转矩时，钢球与钟形壳外滚道和星型套内滚道之间接触，而保持架受到钟形壳内球面及星型套外球面的作用力，所以阻止了钢球从滚道中脱离而出 ^[11,12]。

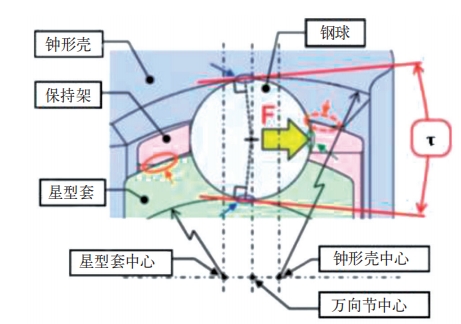
图5 球笼式万向节各部件之间的受力关系

根据上述球笼万向节各部件之间的相互作用关系，分别将钢球与内外滚道之间、保持架与钟形壳内球面及保持架与星型套外球面之间设置为接触关系，摩擦系数为 0.1^[6,8]。另外，考虑到在无摆角状态下传递转矩时，钢球与脱离保持架一侧的保持架内表面保持接触状态，为了改善模型的收敛性，将该保持架内表面与钢球接触区域进行绑定约束。最后，将万向节对称面上施加周期性对称约束，右侧端面施加固定约束，并将万向节的中心与钟形壳外表面进行耦合约束，施加转矩载荷，如图 6 和图 7 所示。

图 6 球笼式万向节接触设置

图 7 球笼式万向节边界设置

2.1 球笼式万向节 CAE 结果分析

对 CAE 分析结果进行后处理，球笼式万向节钢球和内外滚道接触应力发生变化，因钢球与内外滚道具有极高的相似度，所以产生的接触应力椭圆长而窄。在小转矩作用下，内滚道上的接触应力大于钟形壳外滚道上的接触应力，随着输入转矩的增加，内滚道（图 8）和外滚道一侧的接触面产生的弹性变形增加，钢球位置随之上升，并且钢球和内外滚道之间的压力椭圆也随之增大至占据整个内或外滚道侧面，最后椭圆面积超出滚道边缘，此时外滚道与钢球接触状态发生变化，钟形壳外滚道接触应力大于星型套内滚道的接触应力。

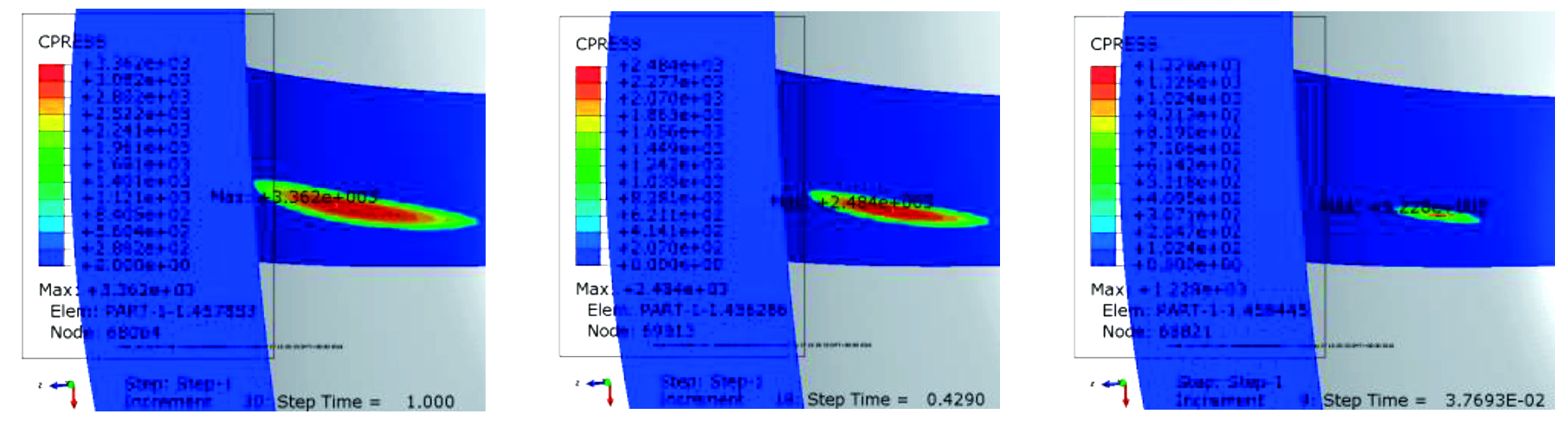
图 8 星型套内滚道在不同转矩作用下的接触应力云图

2.2 CAE 结果与 Hertz 理论计算结果对比与分析

将 CAE 分析结果进行整理，并与 Hertz 理论计算结果进行对比，如图 9 和图 10 可得，在转矩作用下，钢球与星型套内滚道及钟形壳外滚道一侧的接触应力随着输入转矩急剧增长；随着输入转矩的增大，接触应力的增加速率减小，并且 CAE 分析计算得到的钢球与内外滚道之间接触一侧的接触应力与对应的内外滚道上的接触应力基本一致，符合接触理论。另外，内外滚道上，Hertz 理论计算得到的接触应力结果大于 CAE 计算得到的接触应力结果，内滚道上，Hertz 理论计算结果与 CAE 分析计算结果之间的偏差＜ 5%，而外滚道上 , 两者之间的偏差随着载荷的增加而增大，最大偏差接近 25%，剔除外滚道上由于转矩增加而钢球上升，应力椭圆超出轨道边缘，钢球与轨道边缘接触而引起接触状态变化部分。如图 11和图 12 所示，内滚道上，Hertz 理论计算得到的接触应力与 CAE 分析计算的应力椭圆面积结果之间偏差较小，基本＜ 5%，而外滚道上 , 两者之间的偏差先随着载荷的增加而增大，最大偏差接近 26%。

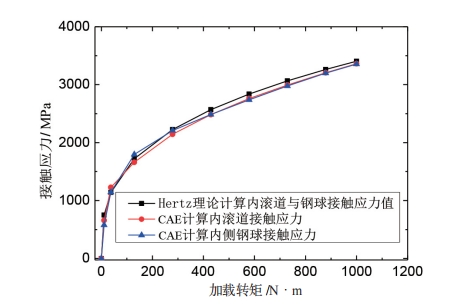
图 9 Hertz 理论与 CAE 计算的外滚道上接触应力结果对比

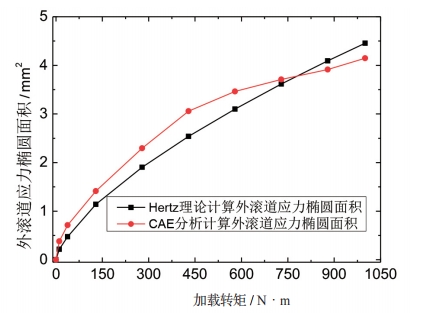
图 10 Hertz 理论与 CAE 计算的内滚道上的接触应力结果对比

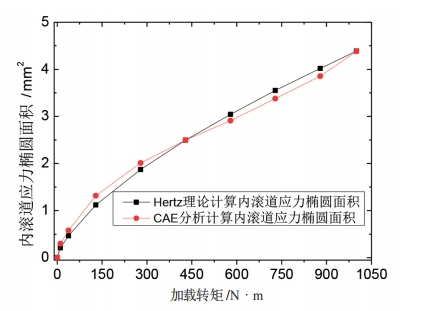
图 11 Hertz 理论与 CAE 计算的外滚道上的应力椭圆面积对比

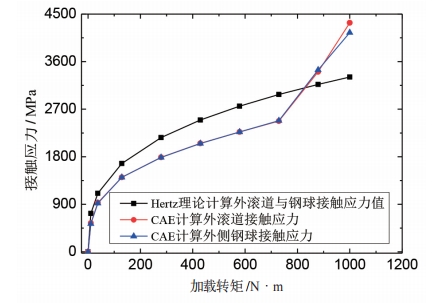
图 12 Hertz 理论与 CAE 计算的内滚道上的应力椭圆面积对比

椭圆偏差的主要原因在于 CAE 计算考虑了摩擦因素和内外滚道的变形而引起接触区域的状态变化，加载过程中钢球上升，传递转矩的有效半径和压力角也随之增大，而 Hertz 理论计算中不能考虑上述因素，因此 CAE计算的应力结果要小于 Hetrz 理论计算的结果。但是伴随着钢球的上升，应力椭圆有部分会超出轨道边缘，使椭圆面积损失，故内外滚道上的应力椭圆面积初始 CAE 分析计算大于 Hertz 理论计算，随着载荷的增加，Hertz 理论计算的应力椭圆面积大于 CAE 分析计算的结果。

3 结论

通过对球笼式万向节的钢球与内外滚动的 CAE 分析，可得到如下结论：1）万向节在传递转矩过程中，钢球与内外滚道之间接触应力在初始状态随着加载转矩快速增加，随着转矩加载到一定程度，接触应力增长速率变缓慢，并且接触区域应力椭圆长而窄；2） CAE分析计算考虑了钢球与内外滚道之间的变形，而 Hetrz理论计算则不考虑上述因素，因而 CAE 分析计算结果更符合实际；3）万向节在传递转矩过程中，钢球位置上升，钢球和内外滚道之间的压力椭圆会占据整个内或外滚道侧面，为防止钢球与滚道因变形过大而导致卡住，滚道边缘处倒角和内外滚道深度必须要控制在一定范围内。

本文建立的球笼式万向节有限元模型能有效地反映球道内部的接触应力和应力椭圆面积，可用于研究万向节内部球道曲率半径和相似度等因素，为万向节的寿命提升提供理论参考。

参考文献

[1] SCHMELZ F, GRAF VON H.-C, SEHEN-THOSS, et al. 万向节与传动轴 [M]. 北京：北京理工大学出版社 , 1998.

[2] KIMATA K, NAGATANI H, IMOTO M, et al. Numericalanalysis and experiments on the characteristic of ball-typeconstant-velocity joints[J]. JSME International Journal,Series C 2004, 47(2):476-754.

[3] SHIN JK, CHOI SR, KIM DW. Contact ratio analysisof the Rzeppa Joint based on full-static modeling[J].Mechanism & Machine theory, 2018, 119:236-251.

[4] PENNESTRI E , VALENTINI PP. Kinematic design andmultibody analysi of Rzeppa pilot-lever joint[J], ProcIMechE Part K: J Multi-body Dynamics, 2008, 222(3):215-227.

[5] CHUL-HEE L, Andresa A. Assessment of Ellipticalconformal hertz analysis applied to constant velocity joints.Tribology[J], Journal of Tribology, 2010 ,132(2):1-3.

[6] 陈静 , 史文库 . 球笼式等速万向节内部接触应力的有限元分析 [J]. 机械强度 , 2006,28(6):937-943.

[7] RYU.I, LIM.T. Finite-element analysis of quasistaticfracture in CV joints under full-turn and full-throttleconditions [J], International Journal of AutomativeTechnology, 2011, 12(2): 199-205.

[8] 候文亮 , 卢曦等 . 极限角度下球笼式等速万向节保持架强度研究 [J]. 机械强度 , 2018,40(4):1002-1006.

[9] 卢曦 , 郑松林 . 球笼式等速万向节结构轻量化设计 [J].机械设计 , 2007,24(6):17-20.

[10] JOHNSON K. L., contact mechanics. Cambridge:Cambridge University Press[M], 1985.

[11] TERUAKI FUJIO. Next-generation hign efficiency fixedtype constant velovity joint"CFJ" [J] .NTN TECHNICALREVIEW, 2013,81:64-67.

[12] 朱卓选 . 高效能球笼式等速万向节的沟道设计 [J]. 轴承 , 2017,10:11-14.

本文为“AI汽车制造业”首发，未经授权不得转载。版权所有，转载请联系小编授权（VOGEL100）。本文作者：陈小敏 夏哲帆，单位：万向钱潮股份公司。责任编辑龚淑娟，责任较对何发。本文转载请注明来源：AI汽车制造业