0 前言

在某款车用嵌入式控制器控制模型的设计中，传统的软件开发流程是先进行需求分析，根据具体的功能需求编写程序，然后做基于台架的程序及数据验证。假如在算法的初级阶段，我们需要验证功能和数据，硬件台架就不是那么方便。

如果能基于MATLAB的Simulink进行建模，并进行算法的验证测试，就方便很多，这样我们就可以在开发初期发现算法中程序错误（BUG），避免在后期发现时，浪费更多的费用及精力来修复这些本可以在前期发现的漏洞。再者，基于Simulink的图形化建模更容易进行仿真，最终会大大提高开发效率。因此，在某款车用嵌入式控制器控制模型的设计开发项目中，我们采用Simulink进行系统的控制算法设计。

1 信号流的模拟

对信号的处理过程有时需要采样处理，例如，一个包含若干个点的数据流按照20kHz的频率发出，在实际的开发过程中，我们需要将它降频到2kHz以下使用。

我们可以在Simulink模块库中寻找相应的信号发生器对该离散的数据信号进行仿真。可以根据需要选择使用重复序列（RepeatingSequence）模块或者从工作空间定义的矩阵读入数据（FromWorkspace）模块等对信号进行模拟，并采用改变采样频率的模块，如速率转换（RateTransition）模块对采样数据进行抽取，并用示波器观察采样前后的数据对比，如图1和图2所示。

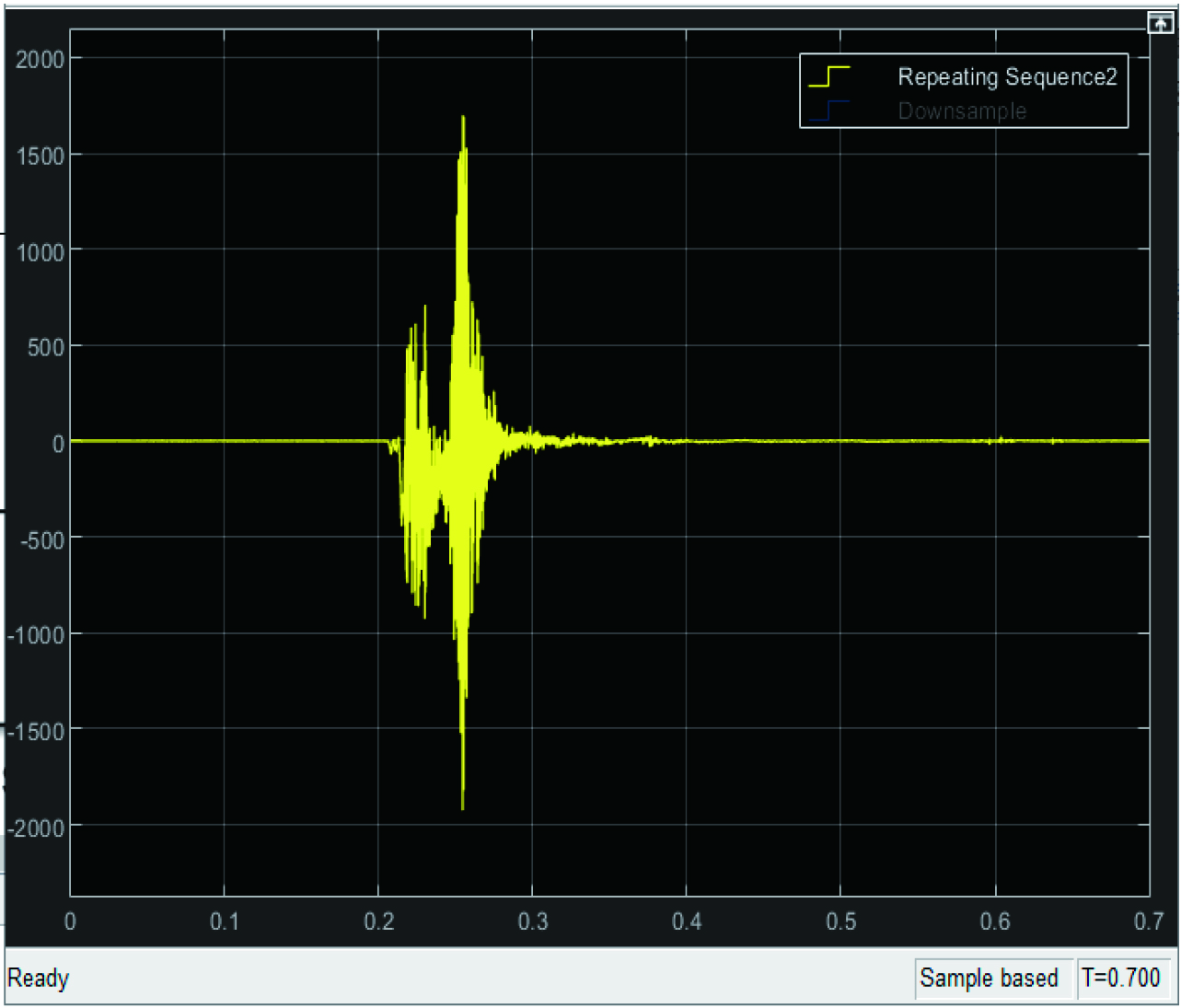
图1 原始信号在20kHz时的仿真

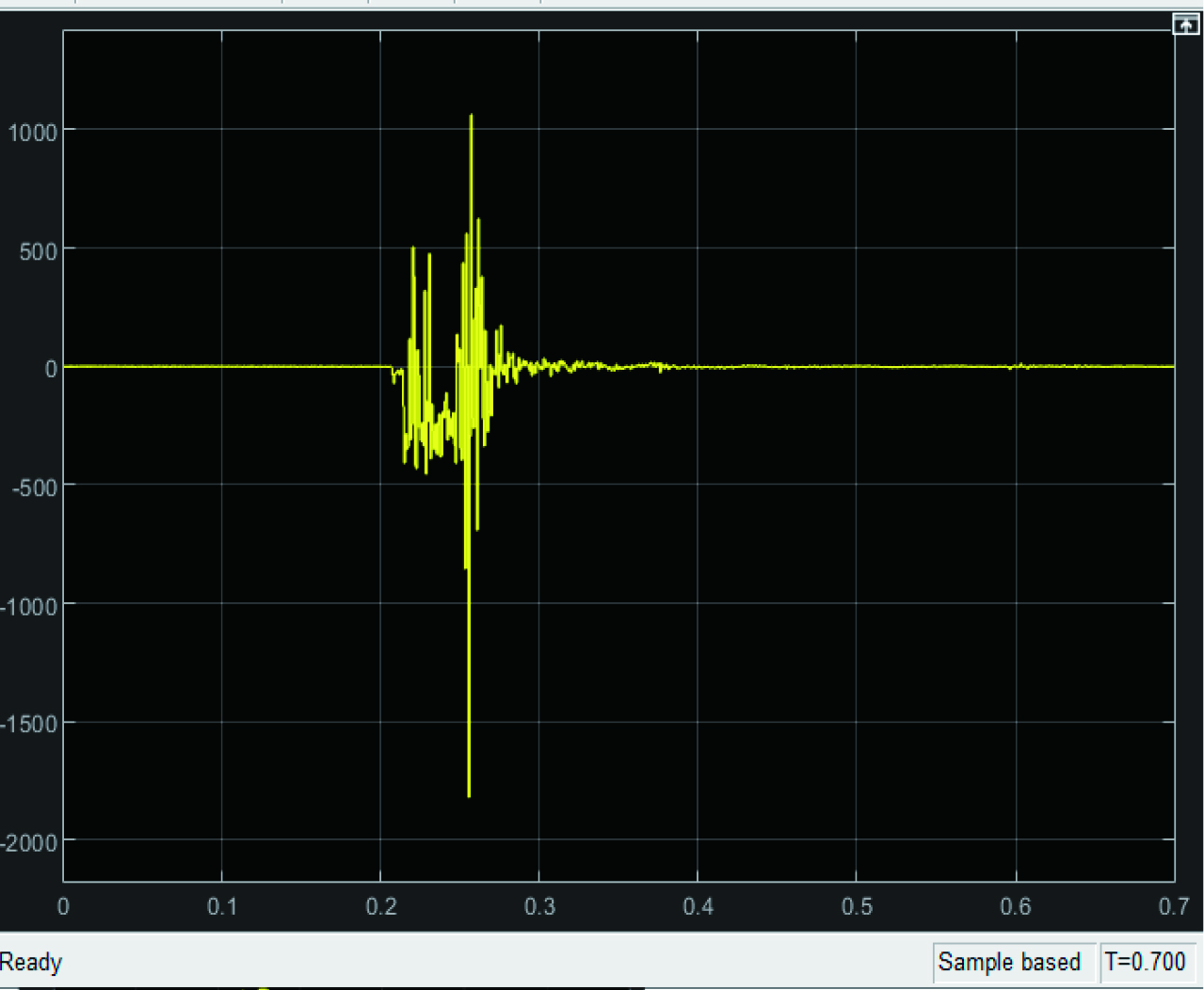
图2 信号降频到2kHz时的仿真

2 信号的低通滤波处理

滤波是对信号的过滤，通过滤除畸变噪声、高频噪声及干扰信号等，尽可能地还原原始数据。常用的滤波有低通滤波、高通滤波及带通或带阻滤波等。我们在数据处理中经常使用低通滤波，低通滤波分为有限脉冲响应滤波器（FIR）和无限脉冲响应滤波器（IIR），如表所示。

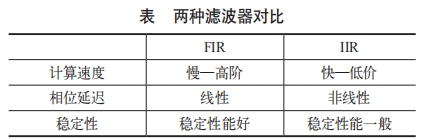
相对于FIR滤波器，IIR滤波器可以使用较低的阶数或项数，这意味着实现相同结果所需的计算量更少，使得IIR滤波器的计算速度更快。若运算数据对时间的响应要求比较严苛，我们可以采用IIR滤波器进行设计。

在设计滤波器之前，我们需要了解信号的采样频率、截止频率以及阶数等参数设置。根据奈奎斯特采样定律：当采样频率fs大于信号中最高频率的2倍时（fs>2fmax），采样之后的数字信号可以完整地保留原始信号中的信息，不发生混叠现象，所以我们的采样频率设置必须大于信号频率2倍以上。

当输入信号的幅值不变，改变输入信号的频率使输出信号降至最大值的0.707倍，此输入信号的频率就是截止频率，也称-3dB截止频率。-3dB截止频率是指信号根据傅里叶变换后，频谱的幅值转换成分贝值20lg（0.707）≈-3dB时的频率。

巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示：

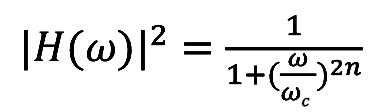
式中，n为滤波器的阶数；ωc为截止频率，即振幅下降为-3dB时的频率。

当滤波器所需的参数计算完成后，我们根据MATLAB自带的工具进行滤波器的设计。在MATLAB的命令窗口键入fdatool或者filterDesigner命令，即可打开滤波器设计窗口，如图3所示。

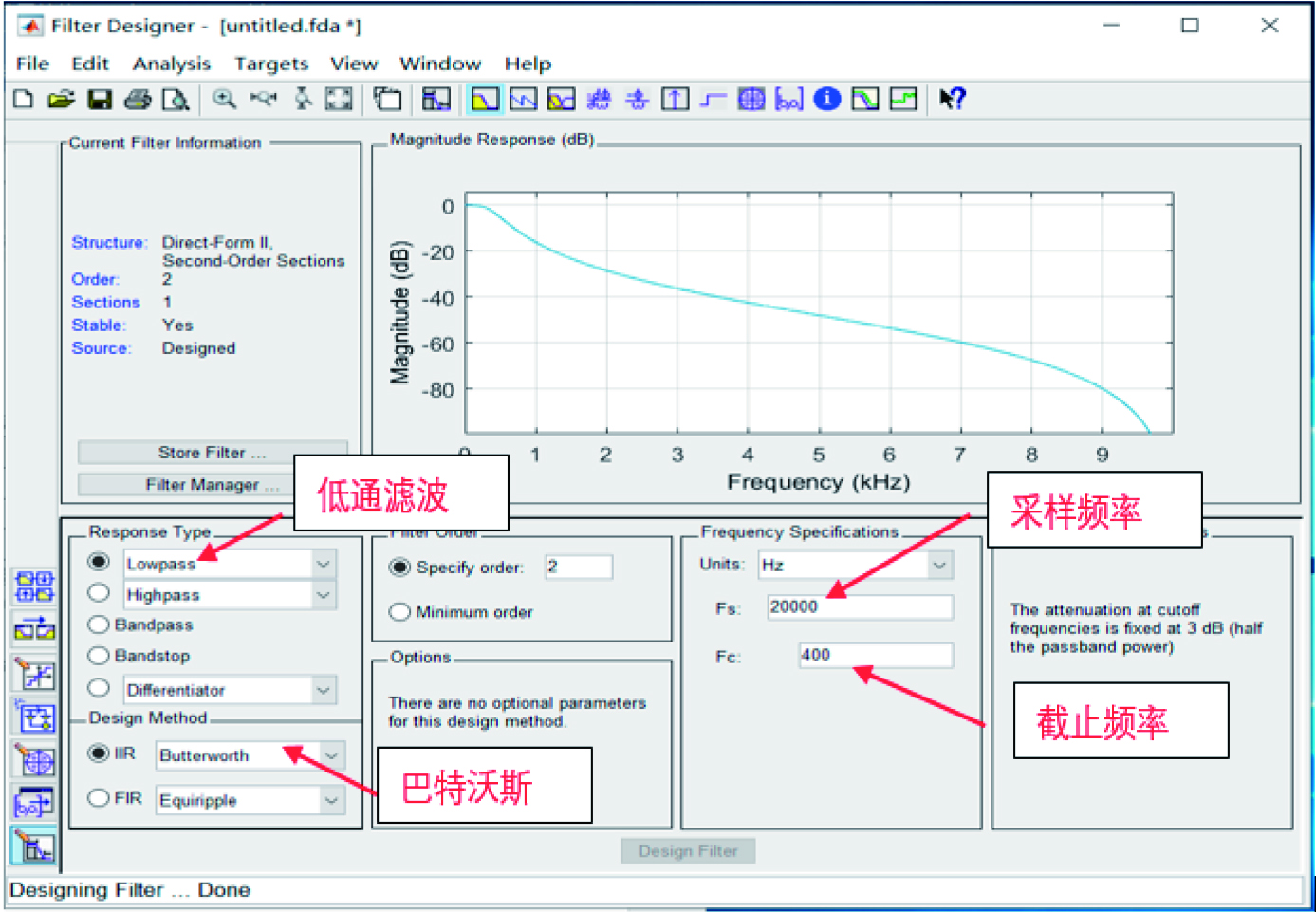
图3 滤波器的设计

根据滤波器的相应类型，我们选择Lowpass低通滤波类型，设计方法选择IIR滤波器中的巴特沃兹滤波。设计完成后，自动生成我们Simulink模型所需要的低通滤波器模块。

从滤波前后的对比图可以看出，信号的噪声干扰明显得到了抑制，如图4所示。对信号进行傅里叶变换后，进行频谱分析，可以看到，在截止频率以后，幅值没有太大的波动，保持在低位，如图5所示。

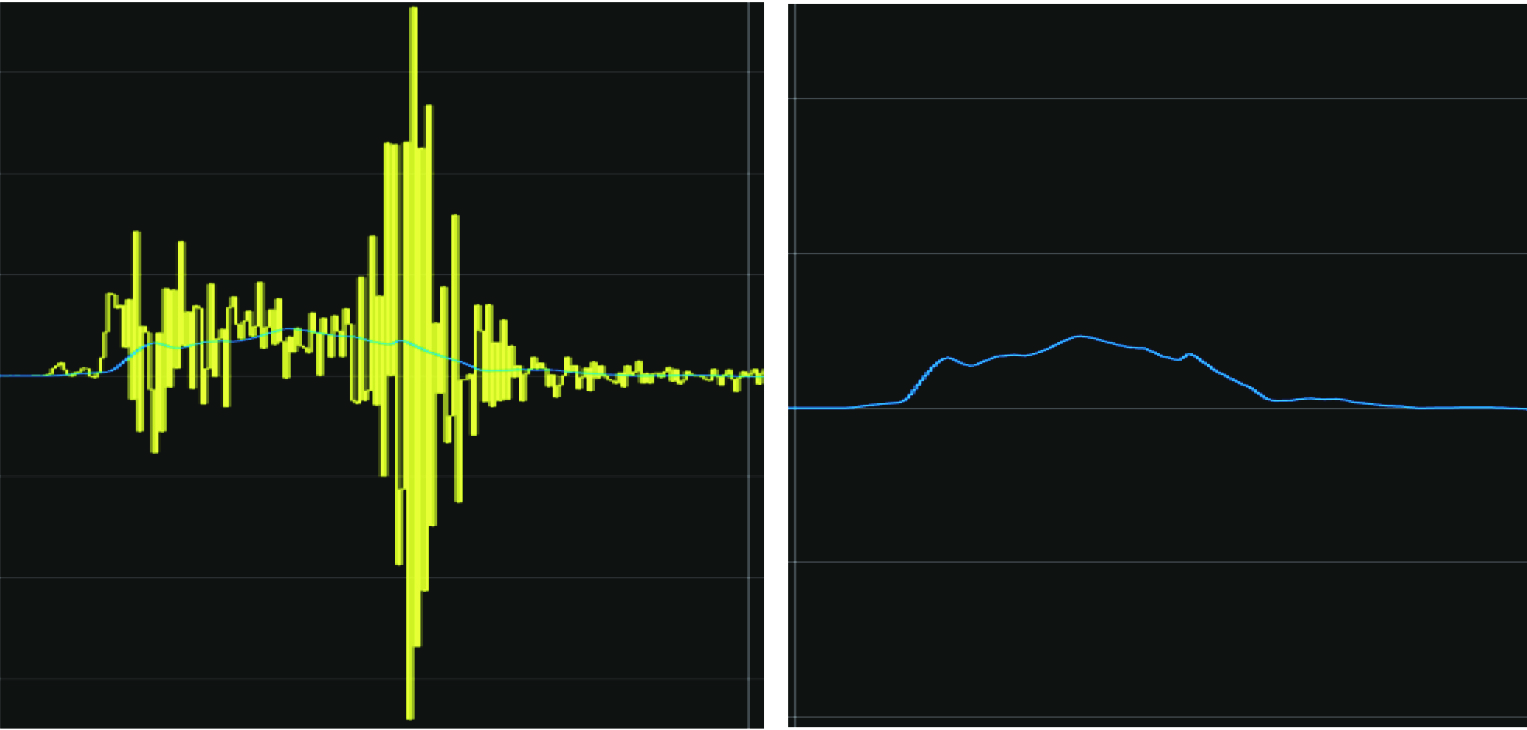
图4 滤波前后对比图和滤波后信号波形

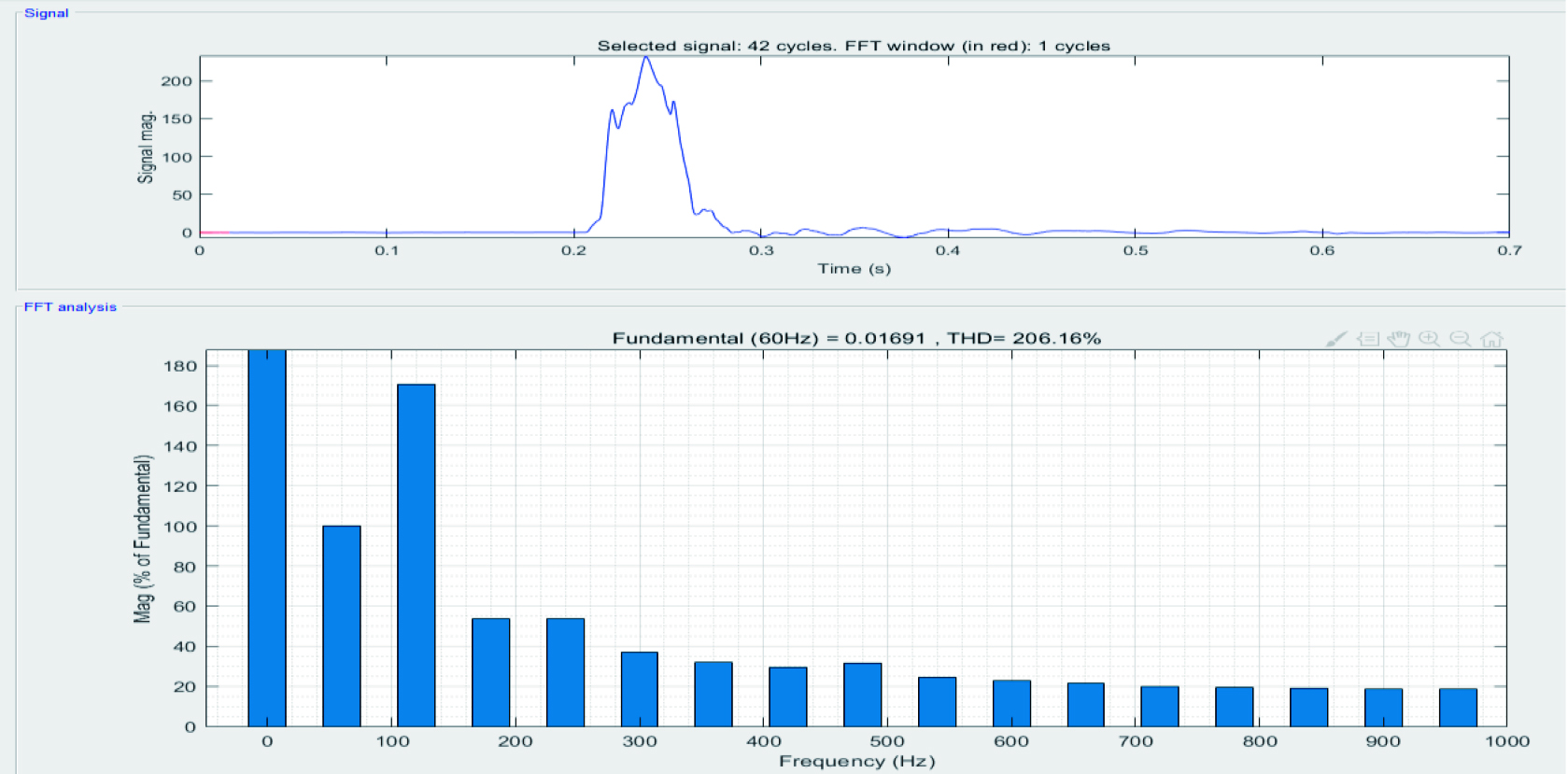
图5 傅里叶变换后的频谱分析

3 低通滤波后的信号处理

信号经过低通滤波后，过滤掉高频噪声，从图4可以看到，信号波形平滑，毛刺较少，在这样的波形基础上，进行信号的再处理，算法模型会比较稳定。如果此时的信号是加速度信号，对信号进行积分后，便可以得到某个时间段内相应的速度信号和位移信号。假定我们设置某个事件触发的阈值为6个单位，当积分后的数据大于等于该阈值时，设定的事件触发。

通过前面步骤的滤波，我们可以看到数据在积分后的曲线比较平滑，没有尖锐的毛刺，这对我们的模型算法的稳定性至关重要，如图6所示。

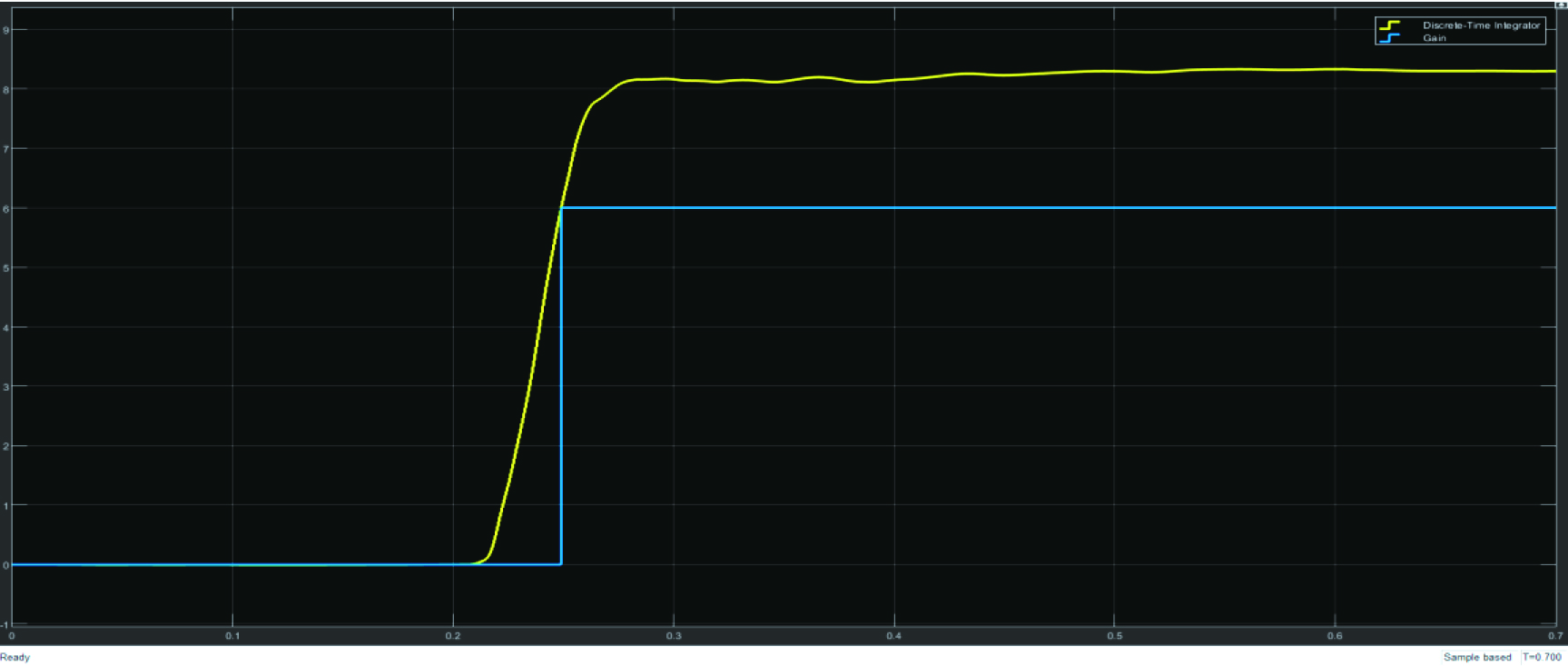
图6 信号触发后的信号观测

4 模型的代码生成

首先，建模后的模型若要生成我们需要的代码，先要能够正常编译通过，然后将模型进行离散，模型中连续的信号将离散化，便于后期集成代码时在任务周期中调用。

生产代码前，还需要对模型进行相关检查，可以使用代码生产检查建议选项,如执行的效率、RAM的有效性检查等。点击运行选定的检查（RunSelectedChecks）,可以对选中的模型进行相应的检查，检查后的结果在报告（Report）框中会有一个总体的体现，我们可以参照此报告对不通过的选项进行整改。设置求解器，如固定步求解，求解器选择离散，根据需要选择运行周期时间。设置完成后，模型生成我们需要代码c文件和h文件。

5 仿真标定

编写MATLAB代码，对建模仿真后的模型进行调用，可根据需要设置循环次数及数据记录。首先定义需要加载的模型名称，调用加载函数，使用SIMOUT函数调用模型进行仿真，我们可以在此函数中设置仿真的时长，以及是否需要加载外部的参数输入，假如我们需要从MATLAB代码中输入参数到Simulink模型，则加载外部输入（LoadExternalInput）选择“ON”，否则选择“OFF”。

如果需要把数据存储，调用SAVE相关的函数，如果需要把仿真后的数据导出到Excel，可以选择XLSWRITE相关的函数，或者相关的仿真数据可以直接在OUT相关的数据结构体中进行查看，在实际应用的过程中我们可以通过多种方式记录仿真后的数据，以便进行后续的数据分析。

6 结论

传统的开发模式，我们使用评审的方法去发现错误，参加评审的同事，往往没有足够的时间了解正在评审的工作，可能会发现一些非常明显的问题，但很难发现一些真正关键的问题。而建模仿真，从效率上来讲，远高于评审，仿真更容易发现设计中的问题。当运行仿真模型时，输入一些设定参数，我们就会得到相应的输出，这样很容易观察到此时的输出是不是我们想要的，输入确定，从而期望的输出结果确定，这便是建模仿真的优势。

Simulink与MATLAB相集成，能够在Simulink中将MATLAB算法融入模型，还能将仿真结果导出至MATLAB做进一步分析。本次设计以建立简单模型并生成代码的形式，展示了建模仿真的基本流程，方法简单，经测试生成的代码可以可靠运行，便于推广。

本文为“AI汽车制造业”首发，未经授权不得转载。版权所有，转载请联系小编授权（VOGEL100）。本文作者：周伟丽 魏敏 田国强，单位：上汽通用五菱汽车股份有限公司。责任编辑龚淑娟，责任较对何发。本文转载请注明来源：AI汽车制造业