AI深度学习及应用在空压系统中的策略优化研究
0 前言
在汽车制造过程中,空压机是不可或缺的关键设备之一,广泛应用于涂装、焊接和冲压等各个生产环节,而且自动化水平越高的生产线对压缩空气的需求量和品质要求也就越高。但空压机的高能耗问题一直是汽车企业面临的一大挑战。如何降低空压机的能耗,提高能源利用效率,已成为当前工业尤其是汽车工业节能领域亟待解决的问题。
传统的空压机能耗优化方法主要依赖于经验调整或固定参数的优化,虽然在一定程度上能够降低能耗,但效果有限且难以适应复杂多变的工业环境。
在空压机深度学习建模的应用方面,研究者们已经取得了一些初步的成果,但对用于工业场景的空压机性能的建模以及优化控制目前还较少有人研究。因此,研究一种新型的建模方法,实现对空压系统的精准控制和优化,具有重要的现实意义和应用价值。
1 建立AI深度学习空压机模型
1.1 数据采集与预处理
在空压机建模过程中,数据收集与处理是至关重要的一步。数据质量直接影响到模型的准确性和泛化能力。因此,我们对空压机运行数据进行了细致的收集和处理。针对空压机建模,将表1的变量纳入模型中。
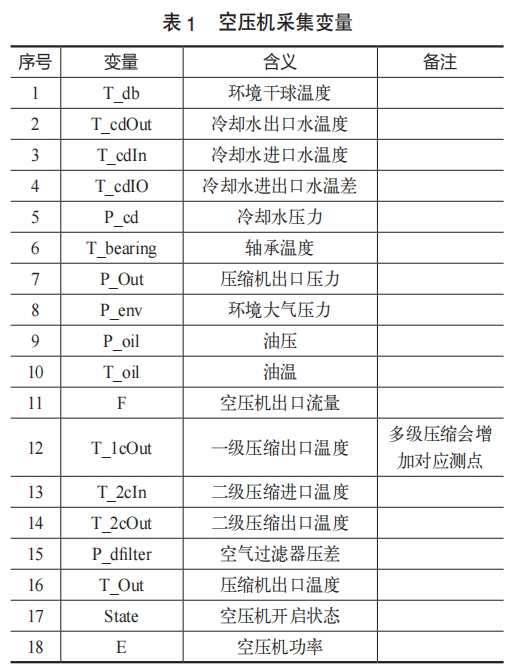
在数据收集完成后,我们进行了数据清洗工作,以去除异常值和重复数据。异常值可能是由于传感器故障、数据传输错误等原因产生的,它们会对模型的训练产生干扰,因此需要被识别并剔除。此处我们使用四分位法,并使用标准的1.5倍IQR值作为阈值,将超出正常范围的数据标记为异常值,并在后续的数据处理中将其排除。同时使用滑动窗口滤波方法,以5个样本作为窗口长度,计算出滑动平均值,对于超出平均值20%的原始样本标记为异常并在后续的处理中将其排除。重复数据则可能是由于数据采集系统的问题而产生的,我们需要去除这些冗余数据,以避免对模型训练造成不必要的负担,我们将一组数据全部为重复的数据和空压机功率数据重复的数据标记为异常,并在后续的数据处理中将其排除。
1.2 多种方法建模对比
(1)机理模型
机理建模使用如下公式:
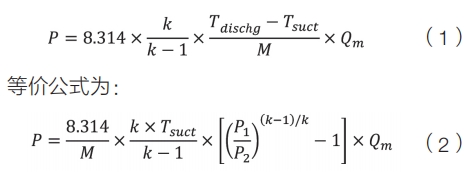
式中,P为压缩机功率,对应表1中的变量18;Tsuct为空压机进口温度(K),对应变量1;Tdischarge为空压机出口温度(K),对应变量14;M为空气摩尔质量(g/mol)28.96;Qm为空压机流量(kg/s),对应变量11;k为空气等熵系数1.4;P2为空压机出口压力,对应变量7;P1为空压机进口压力,对应变量8。
(2)线性回归建模
线性回归的目标是找到一个最佳的直线(在多变量情况下是平面),使得这个直线(平面)与数据点之间的距离最小化。这个距离通常是欧几里得距离,即垂直距离。通过最小二乘法,可以求解线性回归模型的参数,从而实现连续型变量的预测。
线性回归模型可以表示为:
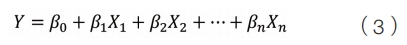
式中,Y是因变量;X1,X2,...,Xn是自变量;β0,β1,β2,...,βn是模型的参数。本文中,将表1中1~17号变量作为输入,18号变量作为输出,并使用最小二乘法求解。
(3)卷积神经网络建模
卷积神经网络(CNN)是一种专门用于处理具有网格结构数据的神经网络,如图像数据。它通过卷积操作提取输入数据的局部特征,并通过层次化的网络结构逐步抽象出更高级的特征表示。CNN在图像识别、目标检测等领域取得了显著的成功。CNN模型通常由卷积层、池化层及全连接层等组成。卷积层负责提取输入数据的局部特征,通过卷积核与输入数据的卷积运算生成特征图。池化层则负责对特征图进行下采样,减少数据的维度和计算量,同时保留重要的特征信息。全连接层则负责将提取的特征映射到输出空间,实现分类或回归等任务。
本文使用两层3*1大小的卷积层、一层3*1大小的池化层和三层全连接层,每层之间均设置激活层,激活层均使用RELU函数。模型输入为表1中1~17号变量,模型输出为18号变量。
(4)建模结果对比
本次建模中,共对5台空压机进行建模测试,对比上述3种建模方法,模型训练从3个指标进行评价(训练结果指标如表2所示),分别是R2拟合系数,R2定义式为:
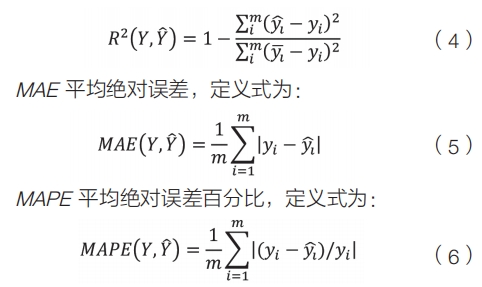
由表2可以得知,CNN模型在5台空压机的建模中,在R2,MAE,MAPE这三个指标中均取得了最佳的结果。同时根据图1所示的5号空压机建模结果,机理建模方法仅对少量工况起到了较好的拟合效果,在900kW功率和1000kW功率附近均出现了较多的预测偏离样本。线性回归和CNN模型均有较好的拟合结果,但从模型指标上看CNN模型的误差更小。综上所述,CNN网络取得了最佳的训练效果,故使用此模型作为优化的基础。
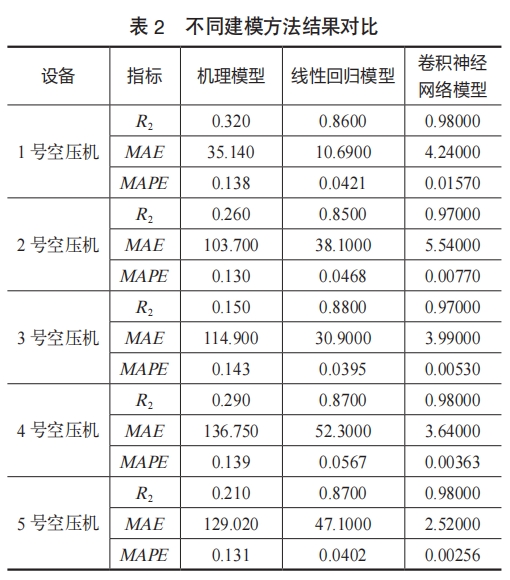
图1 机理模型空压机功率真实值与模型预测值对比
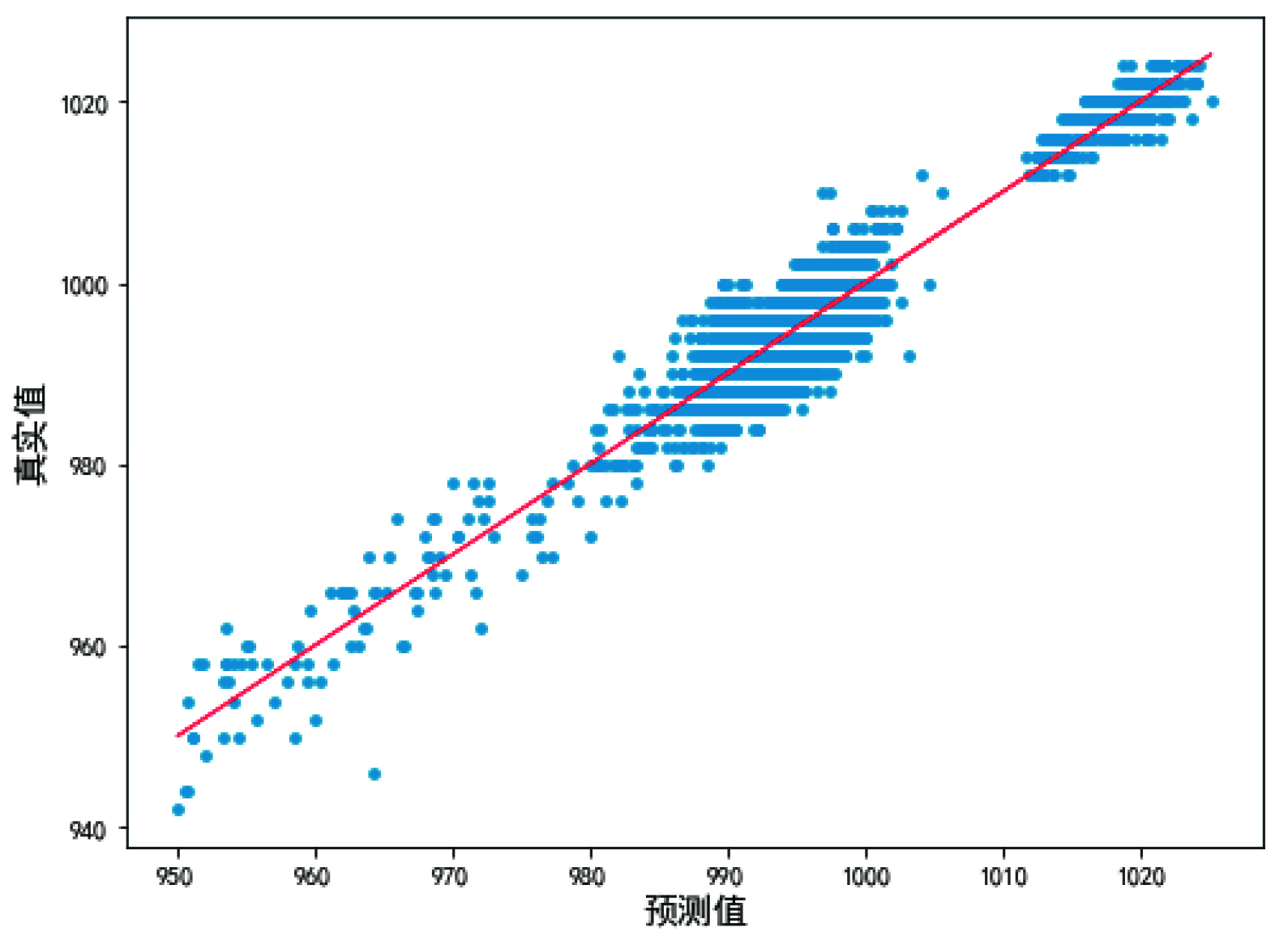
图2 线性回归模型空压机功率真实值与模型预测值对比
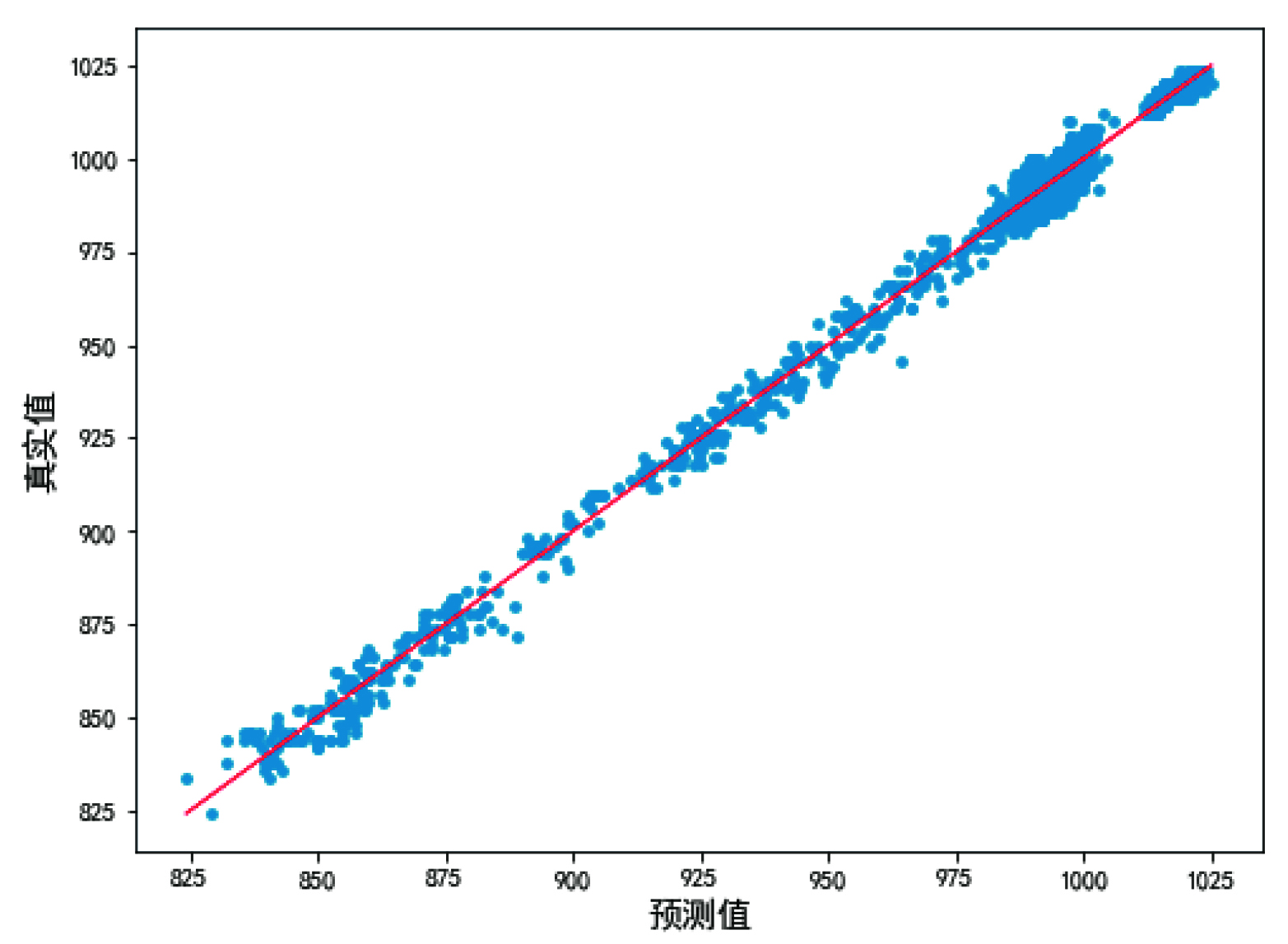
图3 卷积神经网络模型空压机功率真实值与模型预测值对比
2 优化目标及优化算法
选择根据压缩机变量特征和工艺流程分析,空压系统模型的输入为每个空压机模型输入,输出为5个空压机模型输出电功率之和,即:
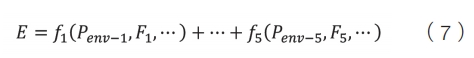
式中,f1~f5为5台空压机模型,优化目标为公式(6)的总功率E最小,即空压系统能耗最低。
遗传算法(GeneticAlgorithm,GA)是一种模拟自然选择和遗传机制的优化算法。它借鉴了生物进化过程中的自然选择和遗传学原理,通过模拟种群的进化过程来搜索问题的最优解。遗传算法的基本思想是将问题的求解过程转化为类似生物进化中的染色体基因的交叉、变异等过程。在求解过程中,遗传算法通过逐代进化来搜索越来越好的近似解,每一代都根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。遗传算法的基本步骤如下。
(1)编码:将问题的解空间转化为遗传算法能够处理的搜索空间,即把问题的可能解从其解空间转换到遗传算法所能处理的搜索空间的转换方法。
(2)初始种群生成:随机生成一组个体作为初始种群,这些个体代表问题的可能解。
(3)适应度评估:根据问题的目标函数,计算每个个体的适应度值,评估其优劣。
(4)选择:根据个体的适应度值,选择一部分优秀个体进入下一代,保证优秀基因得以传递。
(5)交叉(也称“杂交”):将选择出的个体进行配对,并按照一定的概率交换部分基因,生成新的个体。
(6)变异:对交叉产生的个体按照一定的概率改变某些基因的值,以增加种群的多样性。
(7)终止条件判断:若满足终止条件(如达到最大迭代次数、找到满意解等),则算法结束,输出最优解。否则,返回步骤(3)继续迭代。故使用遗传算法对空压系统模型的输入参数进行寻优,使得系统总功率最低的输入参数,即为最佳控制参数。本文中,使用表1输入变量中7空压机出口压力、11空压机出口流量、17空压机开启状态作为可变量,其余输入参数为固定常数取当前实时值,变量18空压机总功率作为寻优目标,同时约束空压系统总供气流量在优化后不能低于当前实际值。种群个数设置为100,初始种群完全随机生成,迭代次数为300次,无其他迭代停止条件。
3 算法验证
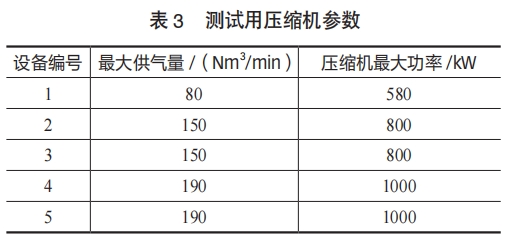
空压机CNN模型训练完成后,使用两个月的新数据对模型进行测试,所有空压机模型指标MAE和MAPE均未超过模型训练时MAE和MAPE,测试集R2指标不低于训练时R2,说明CNN模型表现比较稳定。本文所提到的5台空压机参数见表3。
我们将供气需求量0~240Nm3/min代入模型进行优化计算得到结果如表4所示。
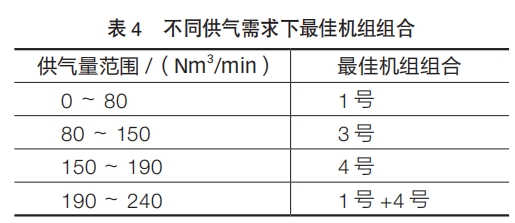
经实际测试,在同样的供气量下CNN模型结合遗传算法给出的最佳组合对比其他机组组合,具有更低的供气能耗。
4 结论
本文尝试了机理模型、线性回归模型以及CNN模型,对比前两种模型,CNN模型在模型精度上有优势。CNN模型结合遗传算法进行空压机控制参数优化,可以找到最佳机组组合以及控制参数,对比其他机组组合方式,此方法推理得到的机组组合整体能耗最低。
参考文献
[1] 王宇.基于数据驱动的空压机故障诊断与性能预测系统研究[D].上海:上海应用技术大学,2021.
[2] 马玉宝,张兴龙,李霖,等.基于数据驱动的空压机健康状态评估[J].石油工程建设,2023,49(1):62-66,87.DOI:10.3969/j.issn.1001-2206.2023.01.012.
[3] 侯大立,王宇,成凡.基于数据驱动的空压机集群智能诊断系统[J].机床与液压,2021,49(12):190-195.<br>HOUDali,WANGYu,CHENGFan.IntelligentDiagnosisSystemofAirCompressorClusterBasedonDatadriven[J].MachineTool&Hydraulics,2021,49(12):190-195
[4]M,U,Hameed,I,A.;SUNDLI,K.HealthMonitoringofAirCompressorsUsingReconstruction-BasedDeepLearningforAnomalyDetectionwithIncreasedTransparency[J].Entropy,2021(23):83.https://doi.org/10.3390/e23010083
[5]胡欢欢.基于HHT和深度学习的船舶空压机故障诊断[D].福建:集美大学,2020.
[6]WUD,BABAKBiA,ALIR,etal.Aircompressorloadforecastingusingartificialneuralnetwork[J].ExpertSystemswithApplications,2021,168,114209,ISSN0957-4174,https://doi.org/10.1016/j.eswa.2020.114209.
[7]SAIDURR,RAHIMN,A,HASANUZZAMAN,M.Areviewoncompressed-airenergyuseandenergysavings[J].RenewableandSustainableEnergyReviews,2010,14(4):1135-1153,ISSN1364-0321,https://doi.org/10.1016/j.rser.2009.11.013.
[8]GHORBANIAN,K,GHOLAMREZAEI,M.Anartificialneuralnetworkapproachtocompressorperformanceprediction[J],AppliedEnergy,2009,86,Issues7–8:1210-1221,ISSN0306-2619,https://doi.org/10.1016/j.apenergy.2008.06.006.
[9]孙志军,薛磊,许阳明,等.深度学习研究综述[J].计算机应用研究,2012,29(8):5.DOI:10.3969/j.issn.1001-3695.2012.08.002.
[10]邹乐强.最小二乘法原理及其简单应用[J].科技信息,2010(23):2.DOI:CNKI:SUN:KJXX.0.2010-23-209.
[11]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[12]丁建立,陈增强,袁著祉.遗传算法与蚂蚁算法的融合[J].计算机研究与发展,2003,40(9):6.DOI:CNKI:SUN:JFYZ.0.2003-09-010.
本文为“AI汽车制造业”首发,未经授权不得转载。版权所有,转载请联系小编授权(VOGEL100)。本文作者:曹轶1 陆炜1 徐亮2 郑铁君2 肖俊3 ,单位:1. 上海大众祥源动力供应有限公司;2.宁波杭州湾新区祥源动力供应有限公司;3.上海龙乾电气科技有限公司 。责任编辑龚淑娟,责任校对何发。本文转载请注明来源:AI汽车制造业
AI汽车制造业
龚淑娟
李峥
相关推荐
-
浅谈人工智能中的图像识别技术
图像识别是人工智能的一个重要领域,是指利用计算机对图像进行处理、分析和理解,以识别各种不同模式的目标和对像的技术。一般工业使用中,采用工业相机拍摄图片,然后再利用软件根据图片灰阶差做进一步识别处理。
2022-02-21
热点文章
-
满足ASIL D的车载12V钠离子电池系统
2026-03-04
-
马勒2030+战略及其中国故事
2026-03-04
-
某新能源电驱系统减速器温升分析与优化
2026-03-05
-
新能源汽车驱动电机恒功率区间转矩衰减的应对方案与工程实践
2026-03-06
-
基于性能分布特性的换档控制标定初值设置方法
2026-03-09
-
车用 PMSM 驱动系统定子电流规划及复合滑模控制
2026-03-10
-
电动汽车交流口电子锁优化设计
2026-03-11
-
电动汽车交流口电子锁优化设计
通过对新国标电动汽车交流充电口电子锁的需求进行分析,本文系统阐述了一款电子锁的理论设计与验证。该方案满足扁平化、高顶出力和高防护等级等要求,解决了目前电子锁普遍存在的高度过高、顶出力不足及防护等级偏低等问题,从而避免充电座外形设计受限,以及因异物顶不出或内部结冰导致功能失效等情况。
作者:叶晓辉
-
车用 PMSM 驱动系统定子电流规划及复合滑模控制
-
基于性能分布特性的换档控制标定初值设置方法
-
新能源汽车驱动电机恒功率区间转矩衰减的应对方案与工程实践
-
某新能源电驱系统减速器温升分析与优化
-
马勒2030+战略及其中国故事















评论
加载更多