线膨胀系数在曲轴精加工工艺中的应用
曲轴作为发动机精度最高的零部件之一,加工过程中尺寸对环境温度的敏感程度非常高。特别是精磨后的直径,受外界环境温度变化的影响非常大。我公司主要生产东风康明斯发动机曲轴,该曲轴的原材料为非调质钢48MnV。本文以康明斯B系列曲轴为例,介绍了如何应用线膨胀系数研究曲轴热变形与环境温度的关系,对曲轴直径的精加工进行现场控制。
试验与分析
线膨胀系数是表征物体热线膨胀性质的物理量,即表征物体受热时其长度、面积和体积增大程度的物理量。为了阐述线膨胀系数的应用过程,分以下几个步骤进行分析:
1.热变形与环境温度的关系
本试验的环境:曲轴精加工设备采用英国兰迪斯LT2HE-1000磨床,加工节拍为20min/件。该磨床配备独立的集中过滤系统,能够保证磨削液始终处于恒温20℃。
检测曲轴直径在加工完成后5 min之内完成。随后,曲轴的直径随自身温度变化而发生变化,曲轴直径加工完8h后趋于稳定。我们要求稳定后的曲轴直径在公差范围内,但实际过程控制中却不可能在加工一件曲轴8h后检测其是否合格。所以,我们需要找到曲轴加工完后5min内检测的直径与曲轴温度稳定后的直径之间的关系,便于在加工完后就能立即检测并判定曲轴直径是否合格。
本试验中关系到曲轴直径变化的最大因素就是曲轴自身的温度变化。曲轴在精加工过程中引起曲轴出现热变形的关联因子主要有以下几个:砂轮切削热的传导;磨削液的温度传导;车间温度的传导。由于曲轴磨削时间只有20min,各种温度的传导仅限于曲轴表面,所以曲轴磨削后的温度是不均匀的,是无法检测数据并用于计算的。
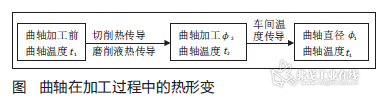
曲轴在加工过程中的热形变是以图1所示的形式进行的。根据材料线膨胀系数公式:
α=(Φ2-Φ1)/Φ0×(t2-t1)
其中,Φ0为20℃恒温条件下检测曲轴的直径。我们要寻求Φ1与Φ2之间的关系,在实际应用中通过控制过程尺寸Φ2,达到控制曲轴最终尺寸Φ1的目的。
根据线膨胀系数的公式可以得出热变形与温度的关系如下:
Φ2-Φ1=Φ0×(t2-t1)×α
首先,由于砂轮切削量是一定的,砂轮的转速、进给速度等参数都是一定的,因此,可以认为砂轮切削热对曲轴热变形的作用也是一定的。其次,磨削液恒温20℃,磨削液对曲轴热变形的作用也是一定的。所以,我们可以将曲轴精加工过程中会造成曲轴热变形的热量当作一个常量Δt,即Δt=t2-t1。轴的温度升高或降低,造成了曲轴的热变形。那么,热变形与温度的关系在这种情况中可以简化为:Φ2-Φ1=Φ0×Δt×α。
2. 线膨胀系数的应用过程
为了找到曲轴精磨过程中热变形与曲轴自身温度变化之间的关系,我们抽取一件曲轴,在曲轴加工完后马上测量与放置8h后再次测量。测量时采用多人对曲轴同一主轴颈的同一测量点进行测量,排除测量系统对试验的影响。
采集过程中,磨削液温度为20℃,室内环境温度为9℃,加工时间20min,具体采集数据如表1所示,可以得出Φ2-Φ1=0.007mm。
我们测得20℃时该曲轴同一部位的直径为Φ83.007m,与室温状态下的检测数据一致,即Φ0=Φ1。参照金属材质,我们查询金属线膨胀系数α=12×10﹣6/℃。由于曲轴精磨后的温度无法测算,那么我们根据以上数据和公式,计算得出:
Δt=0.007/(83.000×12×10﹣6)=7.03℃
根据计算得到在环境温度9℃时,造成曲轴温度变化的影响为7.03℃。那么得到用于控制的精磨直径:
Φ2=Φ1+Φ1×Δt×α
=Φ1+0.000084×Φ1
在曲轴精磨过程中有两个直径需要控制,温度稳定后,要求主轴颈Φ83±0.01mm,连杆颈Φ69±0.01mm。根据以上公式可以得出应用于加工过程直径的名义尺寸为:
(1)主轴颈:83+0.000084×83=83.007mm
(2)连杆颈:69+0.000084×69=69.006mm
为此,我们按照试验后得出的直径公差范围对生产过程进行控制,在终检二次确认直径均符合成品公差要求。
3. 验证直径变化公式
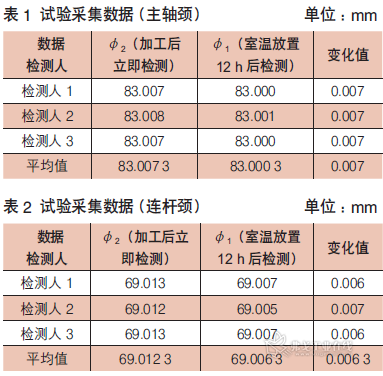
为了进一步验证我们得出的直径变化公式:Φ2=Φ1+0.000084×Φ1,我们按照同样的试验方法,取连杆颈直径作为试验对象采集数据(见表2)。
从表2中可以看出,连杆颈的直径变化量为0.0063mm,与公式计算出的0.006mm非常接近。考虑测量系统的误差,充分验证了以上公式的准确性。
结语
综上所述,可以得出如下结论:
1. 曲轴精加工工艺中,在特定环境下切削热量及水温对曲轴加工尺寸的影响一定。
2. 通过应用线膨胀系数,只需要测定曲轴主轴颈的直径变化量即可计算出连杆颈直径的变化量。
3. 以上试验过程只是验证了一阶段时间内温度对曲轴直径的影响,收集不同室温下温度对直径的影响是一个长期的过程,只有收集了充分的数据,才能制定准确的用于过程控制的尺寸,减少并消除加工过程中温度对直径的影响。
4. 通过测定加工环境温度对曲轴直径的影响,为完善曲轴加工工艺和提高曲轴过程质量提供了可靠的保障。
龚淑娟
李峥
热点文章
-
价值重构 生态竞争
2026-02-26
-
AI驱动下的汽车产业发展趋势及应对策略
2026-02-27
-
“锂欧佩克”的崛起与我国锂资源安全战略研究:挑战、影响与应对路径
2026-02-28
-
新能源车锂电池市场分析-2026年1月
2026-02-24
-
一文理清全主动智能底盘,主动悬架800V和48V之争的真相
2026-02-24
-
罗兰贝格注资Jonas Andrulis新创企业,深度赋能人工智能应用领域
2026-02-24
-
从炫技到生产力,均胜电子打通机器人落地工业场景应用“最后一公里”
2026-02-24
-
“锂欧佩克”的崛起与我国锂资源安全战略研究:挑战、影响与应对路径
锂是新能源汽车与储能系统的关键原材料,其战略价值日益凸显。2025年7月,玻利维亚、阿根廷和智利组建了全球首个锂资源协调机制——“锂欧佩克(LithiumOPEC)”,通过股权管控、上调开采费与推进定价主导等方式,试图重塑全球锂资源供应链的利益分配格局。本文分析其形成背景、运作机制及对我国锂产业链的影响,并从构建自主可控供应体系、推动产业链技术迭代与协同升级、加强国家统筹与海外风险防控以及深化国际合作与全球治理参与四个维度提出应对策略,以增强供应链韧性、降低对外依赖并提升产业话语权,为我国新能源产业高质量发展与资源安全提供支撑。
作者:孙昱晗 宋双 吴喜庆 宋承斌
-
AI驱动下的汽车产业发展趋势及应对策略
-
价值重构 生态竞争
-
AI《汽车制造业》2026-1期
-
欧摩威中国:敏捷应需求,长期创价值
-
坚守与前瞻:桑普拉斯以技术优势赋能汽车行业












评论
加载更多