随着发动机负荷的逐渐增大，曲轴主轴承的单位比压也逐渐增大，这对主轴承的润滑提出了更高的要求。本文基于弹性流体动力学理论，建立了某直列四缸发动机的多体动力学模型。计算结果表明，主轴颈开孔位置优化后，主轴承的润滑性能得到了较好的改善。

发动机连杆大头轴承一般通过开设在曲轴上连通主轴颈和连杆颈的油道进行供油润滑。机油首先由缸体主油道进入主轴承，然后通过主轴颈上的油孔进入曲柄臂内的油道，最后通过连杆颈上的油孔润滑大头轴承。这样就需要在主轴颈和连杆颈上钻油孔，并在曲柄臂内加工连通二者的油道。对于如何确定油孔的位置，以前人们主要考虑工艺性方面的因素，而没有分析其对润滑的影响。随着汽车工业的飞速发展，许多新技术在发动机上逐渐开始应用和推广，如增压、缸内直喷等，这使得发动机的强化程度不断提高，发动机轴承的润滑工况愈加恶劣，任何对润滑有影响的因素都必须充分考虑，主轴颈上油孔的开设位置也成为需要研究的内容。

本文使用AVL Excite Power Unit对某发动机曲轴系建立动力学仿真模型，引入EHD轴承连接副（Elastic-Hydro-Dynamic Joint），综合考虑曲轴轴颈和主轴瓦的表面粗糙度、轴颈和轴瓦的油孔位置、供油压力、曲轴系的动力学行为及缸体轴承座的弹性变形等影响因素，分析主轴承的润滑特性，并通过分析轴承压力的分布状况来优化主轴颈油孔的布置位置，最后比较优化前后轴承润滑的变化情况。

数学模型

本文主要针对流体和结构两部分进行计算，首先将结构有限元的节点位移结果映射到流体网格上，作为流体计算的边界，然后将液体力映射回到结构节点上，得到节点位移，通过不断重复上面的计算过程得到方程收敛解。

1.流体润滑方程

扩展Reynolds方程是进行轴承润滑流体计算的控制方程，其中使用了如下假设：接触表面曲率半径远大于油膜厚度；与粘性剪切力相比，忽略惯性力和体积力；流体为牛顿牛体；流体在界面上无滑动；忽略油膜厚度方向的压力变化。

由以上假设得到控制方程为：

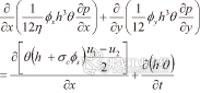
式中

P——油膜压力，单位为Pa；

η——机油动力粘度，单位为Pa.s；

θ——机油填充率；

φx和φy——X和Y方向的压力流量因子，表示表面粗糙度对压力流量的影响；

φs——剪切流量因子，表示表面粗糙度对剪切流量的影响；

u1和u2——轴颈和轴瓦的周向运动速度，单位为m/s；

h——名义油膜厚度，单位为m。

扩展的Reynolds方程考虑了油膜压力、油膜厚度、轴心位置、机油粘度、表面粗糙度和发动机转速等多种因素，合理表达了各种参数之间的关系。

2.运动动力学方程

曲轴主轴承轴颈和轴瓦在载荷与油膜压力共同作用下产生弹性变形，可以用各自的动力学方程算出。

油膜压力作用下曲轴主轴瓦动力学方程为：

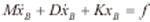
式中 xB——轴瓦位移量，单位为m；

M——轴瓦质量，单位为kg；

K——刚度，单位为N/m；

D——阻尼矩阵，单位为N.s/m；

f——轴瓦所受的油膜压力，

单位为N。

曲轴主轴颈受油膜压力和外载荷共同作用，其动力学方程为：

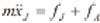
式中 m——曲轴主轴颈质量，单位为kg；

xJ——曲轴主轴颈位移向量，单位为m；

fJ——主轴颈受到的油膜压力，单位为N；

fA——外载荷，单位为N。

仿真模型

计算采用发动机专用软件AVL Excite Power Unit，根据发动机实际结构搭建仿真模型。模型需要考虑整个曲轴系的所有部件，包括曲轴、连杆、活塞、飞轮、减振皮带轮和缸体等。为了减少计算规模，先把这些部件进行模态缩减，只保留各部件的关键节点和相关自由度。连杆大头轴承定义为弹性连接，主轴承定义为弹性流体连接。

计算工况为额定转速4850r/min。设定曲轴旋转轴线为X轴，Z轴为气缸中心线方向。主轴颈油孔的初始开孔位置为0°，工作油温设定为最大油温130℃。从发动机前端往后分别定义为第一、第二、第三、第四和第五主轴承，代号为MB1、MB2、MB3、MB4和MB5。

结果分析

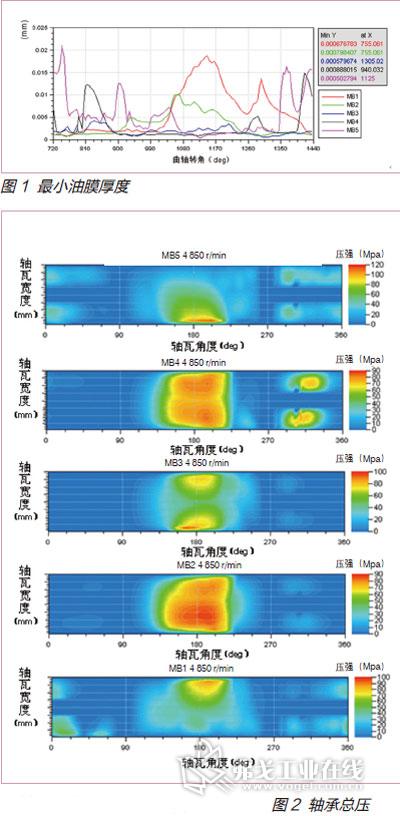
1.最小油膜厚度与轴承总压

对轴承润滑特性的主要考察指标为最小油膜厚度（见图1）和轴承总压（见图2），如果这两个指标能够满足要求，轴承就能工作在一个较好的状态。考虑主轴颈和主轴瓦的表面粗糙度，一般要求主轴承的最小油膜厚度达到0.6～0.8μm。主轴承的承载能力则根据选用轴瓦材料不同而不同，对于本机型所选轴瓦要求最大轴承总压不能超过180MPa。

从图1、图2中可以看出第三和第五主轴承的最小油膜厚度略微小于设计要求，而各个轴承的最大总压则能够满足要求。这说明第三和第五主轴承存在偏磨，需要进行优化。一般解决偏磨的方案是增大轴颈尺寸以及更改轴颈、轴瓦的型线。增大轴颈尺寸能够增加曲轴刚度，减小弯曲变形，但这要求整机也要做相应的更改，同时摩擦功会增大，不能作为改进的措施。轴颈和轴瓦型线改变需要改变加工工艺，增加了零部件的成本。经过综合考虑，优化方案确定为变更主轴颈油孔位置，以达到采取最小的变动来满足设计要求的目的。

2.摩擦特性分析

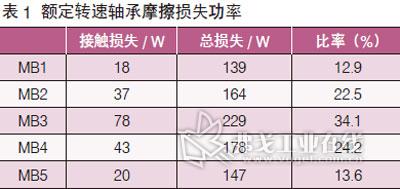
主轴承的摩擦损失分为流体摩擦损失和接触摩擦损失。流体摩擦损失是由于流体流动时内部剪切力作用而产生的。接触摩擦损失则是两固体结构未能完全分离，相互摩擦所致。功率损失比定义的是主轴承由于粗暴接触产生的摩擦损失与总的摩擦损失之比，这个指标反映了轴承摩擦磨损的情况，也是整机摩擦功评价的重要内容。

由表1可以看出，第二、第三和第四主轴承的摩擦损失较大，接触摩擦所占总损失的比重也较大，都超过了20%，第三主轴颈达到了34.1%，需要进行改进。同样考虑各种因素，改进方案也定为修改主轴颈油孔位置。

主轴颈油孔位置优化

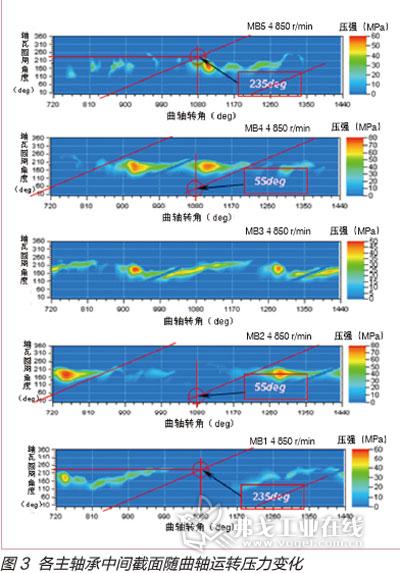
对主轴颈油孔进行优化必须掌握轴颈上各部位在各个曲轴转角时刻的压力分布，然后选择在一个发动机工作循环范围内油膜压力分布都较小的点作为油孔开设位置。在模型中采用EHD连接副，计算可以得出轴颈上所有点各个时刻的压力值。主轴承在轴向方向，一般中间位置的油压较低，因此常将油孔位置开设在主轴颈轴向长度的中间位置，设计只要确定油孔在圆周方向的开设角度即可。

图3为额定转速下各主轴承中间截面各位置点随曲轴转角变化的压力变化情况。根据压力分布，重新选择主轴颈油孔位置，主轴颈油孔选择整个工作循环中压力分布小的位置。图中的斜线为主轴颈上一点的轨迹线，通过平移轨迹线找出在整个工作循环内压力均较小的线，确定油孔位置。如图分别选择一、五主轴颈油孔位置为235°，第二、四主轴颈为55°，因为是四缸机，第三主轴颈不需要开设油孔。

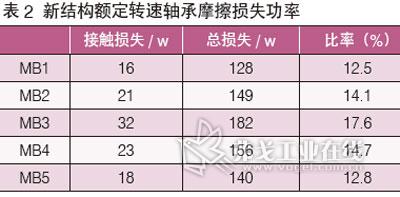
对调整油孔后的运动结构重新进行计算，得到额定转速点各个主轴承摩擦功率如表2所示。

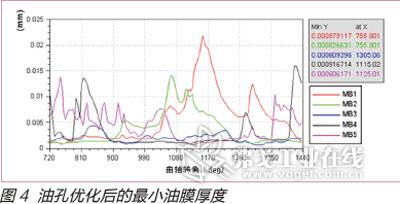
从表2可以看出各轴承摩擦功率都一定程度减小，摩擦损失占总损失的比率也都减小。其中第二、第三和第四主轴承接触损失减小较为明显，最大下降达到77.6%，满足设计要求，润滑状态得到改善。优化油孔位置后各主轴承最小油膜厚度如图4所示，可以看出第三与第五主轴承的油膜厚度增加到0.6mm以上，润滑状况得到改善，油膜能够有效形成，这样摩擦功率损失的变化也能很好对应。

结语

采用弹性流体动力学计算方法，能够全面考虑影响轴承润滑的多种影响因素，包括轴颈和轴瓦的表面粗糙度、润滑油孔位置以及结构体的弹性变形等。额定转速点，第二、第三和第四主轴承的摩擦损失较大，接触摩擦所占总损失的比重也较大，第三主轴承达到34.1%。修改主轴颈油孔开孔位置，各轴承接触摩擦损失较原结构都有一定减小，其中第三主轴承减小达到77.6%。各主轴承最小油膜厚度都能满足要求，润滑良好。