作为一种科学的、规范的方法，能力验证在现代制造设备的评定中越来越被人们所重视，在汽车制造业中应用尤其广泛。能力验证在产品质量的过程控制中发挥着重要作用。

在以批量生产为特征的企业中，自动化程度高、精度高和效率高的专用制造设备是贯彻生产工艺的主体。在这类设备的诸项技术指标中，所完成产品的制造质量，如由机床加工出的工件所达到的精度等，无疑是最关键的一项指标。但长期以来，无论是新设备的验收还是日常生产中，对这项指标的评定一直采用抽样检验的方式，即对试加工的一批产品进行检测，若实测结果全部在公差范围以内，就认为这项指标合格，其加工能力满足要求。至于如何进行抽检，如何根据测量结果的分布状态做出确切的评价，则没有明确的、统一的规定。

上述的传统评定方法实质上是一种定性的、不严密的方法。对于现代制造业，特别是生产批量大、质量要求高的那些行业（如汽车、内燃机、空调压缩机等），由于需要确切地掌握制造设备所具有的保证产品质量的能力，并要求给予定量的表述，这种传统方式的不足、局限性便显现出来。因此，急需建立一种更科学、更严谨的评定方法，以满足和适应现代制造业所配备的专用制造设备对验收和日常生产所提出的要求。

以机器能力指数Cm作为评价指标的设备能力验证方法由于顺应了现代制造业的这种需要,故自20世纪90年代以来已在国际上流行,并被越来越多的国内外企业所采用。

过程能力指数Cp和机器能力指数Cm

工序是制造零部件的基本环节，是形成产品的基础，如果生产过程中每一道工序的质量都很好，那么产品质量也就有了保证。所谓工序质量是指本道工序应有的制造质量，即在稳定状态下所具有的保证产品质量的能力，它取决于设备、材料、操作者、工艺和环境等五方面，是五项相互独立因素综合影响的结果。过程能力的表述建立在对质量特性值离散程度的研究的基础上，采用过程能力指数CP这一评定指标来定量地反映工序能力满足产品质量（如零件的尺寸公差）要求的程度。其计算公式为：

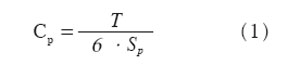
上式中：

T——公差范围

Sp——总体标准偏差（工序中各项因素的综合影响）

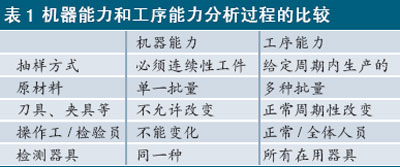
机器能力指数Cm反映了在工序稳定的情况下，上述五项相互独立因素中的第一项（设备）的影响。机器能力是工序能力的重要组成部分，对于自动化程度很高的批量生产过程，机器能力显得尤为重要。尽管在技术上，它与前述工序能力分析一样，都是建立在数理统计基础上，以质量特性值分布的标准偏差S来表征，但机器能力指数Cm是对五大因素之一的微观分析，而过程能力指数Cp是综合了诸项因素的影响，因此在具体处理上有区别，表1为机器能力和工序能力的分析过程的比较。

那么，何时需对生产线上的专用制造设备进行机器能力指数的测试呢？在以下三种情况下需测算Cm值，进而按评定规则对专用制造设备的能力做出判断，并采取相应的措施。

● 新设备的验收过程中；

● 在生产过程中对工序能力进行监控时，出现“过程能力”异常情况，为查找原因而进行分析、采取措施时；

●  用作设备维修验收的依据之一，即在对专用机床进行大修的前后及在开展对设备本身或相关工装、夹具（刀具）进行技术改造时，为了评价改造的效果。

机器能力指数Cm和Cmk的获取

在作为随机变量的被测量服从正态分布的情况下（这种情况占极大多数），求取机器能力指数Cm 与计算过程能力指数CP相似，也是采用质量特性值（被测量）分布的标准偏差来表征的，简单地以符号S表示。

S可直接由质量特性值的实测数据求得，而表1则指出了实测过程必须满足的基本要求，具体的做法为：将被评定的专用制造设备调整至规定状态，经若干小时无故障空运转，再完成一定数量的零部件制作。然后取50个连续生产出来的工件作为样本，把它们送至相应测量仪器进行检测，由此获得一组质量特性值的实测数据，并按熟知的方法求出平均值和标准偏差S：

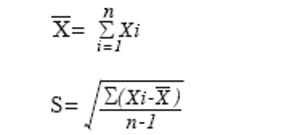
机器能力指数Cm定量地表达了设备所具有的满足产品质量的能力，其计算公式为：

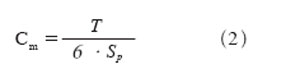
式中T表示被测量公差，确切地讲是被测量上、下极限值之差，即公差范围，其计算方法为T=T0-Tu。此处T0为公差上限，Tu为公差下限。

式（3）的成立有以下前提：被测量实测数据的分布中心必须与其公差中心（设计中所规定的被测量中间值）重合。只有在这个条件下，Cm=T/6·s才有意义。因为由正态分布的性质可知，当两个中心重合时，如Cm=1，表明将有99.73%的产品被测量特性值会落在公差T范围以内而成为合格品；当Cm<1时，废品率增加；而Cm>1时，废品率减少，所以Cm值的概念是很直观和明确的。但是，实际上这个条件是难于满足的。以机械加工为例，工件尺寸的分布中心，一般取决于设备的调整和其他一些因素，而要把设备调到使两个中心重合，绝不是件容易的事。事实上，两个中心或多或少都存在偏离，而不管是左偏还是右偏，都将导致废品率增加，从而相当于降低了机器能力指数Cm值，由于正态分布曲线是对称的，故不论左偏或右偏，只要偏离量相同，对合格品率减少、废品率增加的影响也相同，也就是造成Cm值降低的程度是相同的。由此可见，按（2）式求取的机器能力指数Cm需根据实际情况进行修正。

令偏离量为Bi，Bi可由前面求出的平均值x和被测量的理论中间值（公差中心值）Xs得到，计算方法为：

Bi=|X-Xs|

经修正后的机器能力指数用Cmk表示，计算方法为：

Cmk=Cm（1 - K）               （3）

式中的K称为修正系数或偏离系数，其值为K=2Bi/T。故（3）式也可以表达为:

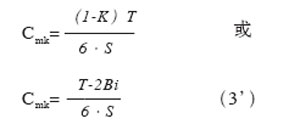
从式（3）和（3’）可看出，只要两中心不重合，存在偏离情况，就存在Cmk<Cm的关系，导致机器能力指数下降；只有Bi=0时，才能使Cmk=Cm。

设备能力验证

根据求出的机器能力指数Cm值，可对被评定的专用制造设备予以能力验证，即对其所具有的保证产品质量的能力作出评价。但根据被测量的具体情况，还有些不同。

● 被测量的公差双向公差

在这种情况下，对专用制造设备的能力验证，若为新设备验收阶段，规定：

Cm≥2.0       Cmk≥1.67     ( 4 )

若是对在用的制造设备进行评定以及对经过维修或技术改造后的设备做验收，则要求：

Cmk≥1.33      Cmk≥1.33           （4’）

在实际求取机器能力指数Cmk时，使用部门往往把式（3’）改写成更加直观、明确的形式：

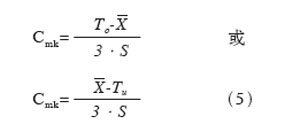
如前所述，式（5）中的To和Tu分别对应于公差上限和公差下限。

● 被测量的公差为单向上公差或单向下公差

在这两种情况下，若进行新设备验收过程中的能力验证，规定：

Cmk≥1.67                     （6）

而对在用设备进行评定以及对经过维修或技术改造后的设备做验证，则要求：

Cmk≥1.33                     （6’）

类似于被测量公差为双向时的情况，在实际求取机器能力指数Cmk时，往往写成如式（5）般更加直观、明确的形式。

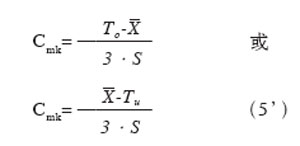
式（5’）中的前面一个对应于被测量为单向上公差的情况，后面一个对应于被测量为单向下公差的情况。

注意：当产品的质量特性值，即其被测量为单向公差时，对相应的专用制造设备进行能力验证时，只要求对机器能力指数Cmk是否达到规定要求作为评价，不再需要求取Cm值。这是为什么？

单向公差大量存在于机械制造中，如加工外径、加工内孔等。操作者为求保险，对前者往往向公差的上限靠，而对后者则向公差下向靠。这种不按公差中心加工的现象虽不会改变制作出的工件的合格性，但对整批产品来讲，其配合状态必然受到影响，从而降低了质量水平。从统计学的角度，则是人为地造成了正态分布中心的偏移，即所谓的“偏态分布”。在这种情况下，相应的专用机床的机器能力指数Cm值再高也没有意义。为了有效地制约这种现象带来的不良后果，此种情况下的评定指标只用Cmk。

生产过程监控中的设备能力验证

综合上述情况，并综合对工艺过程的监控要求，可归纳为表2。

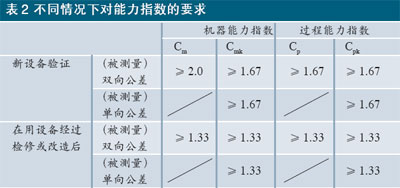
表2既规定了不同情况下机器能力指数的控制要求，又明确指出了对应的过程能力指数Cp应该达到的数值。至于对生产过程进行监控中出现工序能力异常情况时，设定的控制要求如下：

（1）当Cp＞1.33时, 即认为此时在工序中的机器能力是充分的；

（2） 当1.0≤Cp＜1.33时，即认为工序运行出现异常，此时需做机器能力指数Cm的测算，若1.0≤Cp＜1.33，就应该判定该专用机床能力不足，必须安排检修，如果仍继续用于生产，则需大大提高制成品的抽验频次，甚至实行全数控制；

（3）当Cp＜1.0，表明工序运行中的过程能力已不足，此时若算出机器能力指数Cm＜1.0，则应该采取紧急措施，对专用机床进行检修，必要时还应实施相应的追溯措施，以消除混入不合格品的可能性。

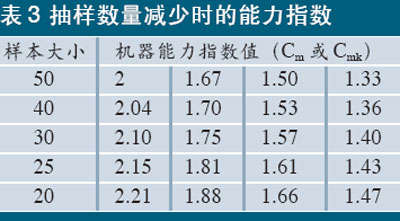
在进行机器能力指数（过程能力指数亦然）评定时，若样本数量减少，根据数理统计原理，此时的Cm（Cmk）值将相应放大，以确保被判定的专用制造设备处于相当的能力水平，表3对此作出了具体的规定。