概念设计阶段车架的结构方案

参考某一同类型车架，考虑到车身安装和其他总成的布置，将概念设计阶段的车架大致结构拟定如下：选用框架式平行梯形车架结构，由2根左右分开的纵梁和8根横梁组成，全长6.3m、宽0.8m、轴距3.65m。各梁的大致形状尺寸及板材厚度如表1所示。

除第3、4根横梁外，其他各横梁的尺寸与参考的同类型车架几乎相同。由于参考车架的第3、4根横梁为上下两片形状复杂的钢板组合而成，无法用梁单元模拟，在概念车架中将之改用两根方型截面的等直梁代替。第1、6横梁为非等截面梁，其宽和高分别由两个尺寸表示。参考车架纵梁的前后两段和中间段的连接采用的是线性渐变的截面，在概念车架中用一等直梁来代替，等直梁的高度等于渐变梁的中间高度。纵横梁上所有的孔及连接板都不予以考虑。

车架的有限元模型

为了后续的优化设计，必须对车架进行参数化建模。选择表1中车架纵横梁的截面尺寸为模型参数，先建立左半个车架的几何模型，选用ANSYS中的二节点12自由度梁单元BEAM188号单元采用不同的梁单元截面形式对其进行网格剖分；再将左边的几何模型和网格模型进行映射得到右边车架模型，最终合并对称面上的节点使左右车架模型“牢固的”“粘结起来”。

在ANSYS中用BEAM188单元实施网格剖分时，为了保证单元的正确方向，应事先定义该单元的方向点并检查所要剖分的线的法向。单元截面形状和偏置量需用命令SECTYPE、SECOFFSET和SECDATA设定。单元总数为312，节点总数为626。网格剖分并映射后车架模型如图1所示。图中显示出了梁单元的截面形状。

图1  车架的有限元模型

边界条件

车架刚度有多种，其中最重要的是车架的弯曲刚度和扭转刚度。参照车架的刚度试验方法确定车架弯扭刚度的边界条件。

1. 弯曲工况的边界条件

计算时约束前后桥在车架纵梁上的竖直投影点的垂直位移，让车架形成一简支梁结构，并在前后支承点中点处加一垂直向下的力，让车架产生纯弯曲变形，如图2所示。

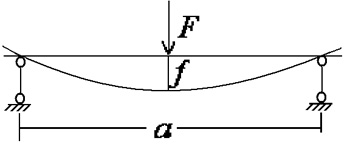
图2  车架弯曲刚度计算

车架弯曲刚度计算公式为：

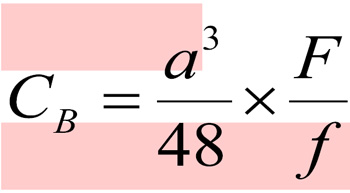                          ①

其中：C_B，弯曲刚度（N/m²）；

F，集中载荷（N）；

A，轴距（m）；

f，载荷作用点处的挠度（m）。

图3为车架有限元模型弯曲工况边界条件示意图。

图3  车架垂直弯曲工况的边界条件

2. 扭转工况的边界条件

约束前桥在车架左纵梁上的竖直投影点的垂直位移，约束后桥在车架右纵梁上的竖直投影点的垂直位移，在后桥在车架左纵梁上的竖直投影点上施加一垂直向上的载荷，让车架产生纯扭转变形，如图4所示。车架的扭转刚度计算公式为：

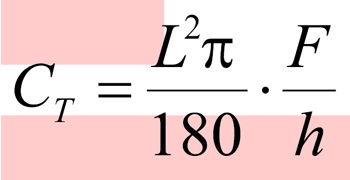                                ②

其中：C_T，扭转刚度（N·m/°）；

F，载荷（N）；

L，力臂（m）；

h，挠度（m）

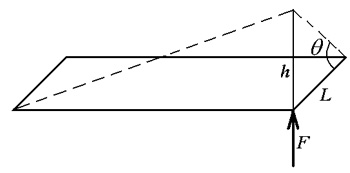
图4  车架扭转刚度计算

图5为车架有限元模型扭转工况边界条件示意图。

图5  前后扭转工况的车架边界条件

求解结果与分析

1.模态的计算结果

用Block Lanczos法提取自由振动时的前5阶固有频率，频率范围0.05～50Hz。车架的前五阶固有频率及振型见表2。相应的振型图如图6～11所示。

 
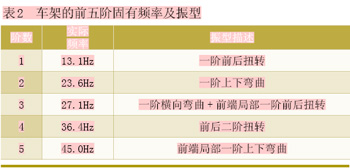
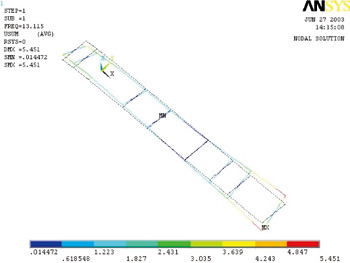
图6  一阶固有频率对应振型

 
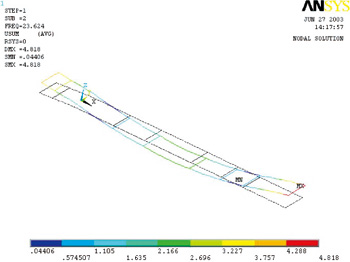
图7  二阶固有频率对应振型

 
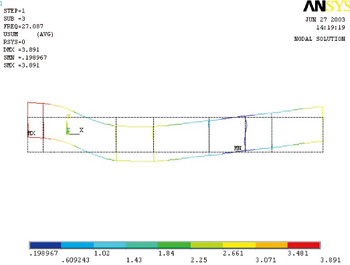
图8  三阶固有频率对应振型（俯视）

 
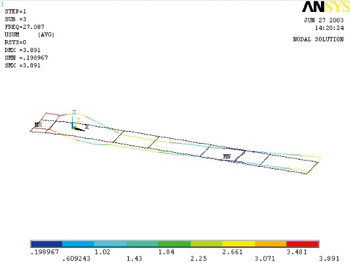
图9  三阶固有频率对应振型（全视图）

 
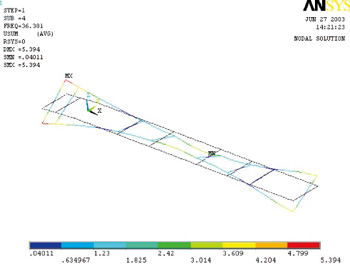
图10  四阶固有频率对应振型

 
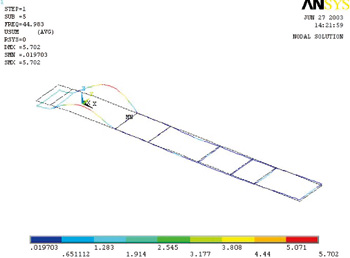
图11  五阶固有频率对应振型

2.弯扭刚度计算结果

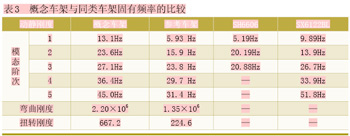
在F＝1 000N时车架弯曲工况载荷作用点处的挠度为0.4595mm；在F＝1 000N时车架扭转工况载荷作用点处的挠度为13.94mm。带入公式①、②中计算得：弯曲刚度为2.2×106N·m2，扭转刚度为667.2N·m/°。

3.结果分析

该概念车架和其他车架动静刚度的比较如表3所示：

经对比，概念车架的固有频率明显高于其他同类车架。分析车架振型发现：该车架第二横梁和第三横梁之间是薄弱环节，在第三阶固有频率和第五阶固有频率下都会发生明显的局部振动。但在整车中该区域会安装发动机和驾驶室，它们对车架刚度都有显著影响，特别是发动机。当发动机与车架的连接刚度较大且采用四点支撑时，会显著的提高该区域的车架（整体）刚度，尤其是扭转刚度，因而该概念车架的这一不足可以得到部分弥补。

对比参考车架的弯扭刚度，概念车架的值也偏高。

优化设计

取纵、横梁截面的长、宽和高共20个尺寸作为设计变量。以车架总体积最小为目标函数对该车架进行弯曲、扭转刚度和一阶扭转频率等综合性能方面的优化。分别选取车架的弯曲、扭转刚度及一阶扭转频率值为状态变量。优化时，参考同类车架，将概念车架的动静刚度适当的扩大，取弯曲工况下力的作用点最大位移不超过0.6mm，扭转工况的力的作用点最大位移不超过16mm，一阶固有频率的下限取11Hz。

采用ANSYS中的一阶优化方法，对比优化前后的参数变化情况，可以得到以下结论：

1.车架模型经过11次迭代后收敛。优化后，车架的重量减轻了12.5%。

2.车架的弯曲刚度和扭转刚度均有降低，其中，弯曲刚度降低29.2%，扭转刚度降低11.3%；车架的一阶固有频率变化仅为2.67%。

3.对弯曲和扭转刚度影响最大的是纵梁前后段的截面尺寸B1和H11。其余各梁的截面尺寸也有不同程度的改变。

结语

本文利用工程分析软件ANSYS计算了某一概念设计阶段车架的静态弯曲刚度、扭转刚度以及自由振动时的前五阶固有频率和相应振型，其动静刚度性能指标均超过同类车架。通过以车架纵、横梁截面尺寸为设计变量进行了优化设计，使该车架减重12.5%。