荷兰国家应用科学研究院下属的综合车辆安全局对现代控制方法在综合车辆动态控制（IVDC）领域的应用进行了调查，并将此作为安全框架之外的一个战略性研究课题。

综合车辆动态控制的研究目的是通过最大化制动系统、悬架系统和转向系统等车辆系统之间的协同作用，实现车辆性能优化，从而改善所有驾乘状态下的车辆安全和舒适性。本文介绍了开发和试验性评估中，用于稳定性控制的最佳综合车辆动态控制方略。此外，本文还介绍了所使用的控制器结构、车辆和轮胎模型、状态相关黎卡提方程控制技术方法及对所开发的控制器的试验性评估等。

控制车辆横摆运动和对纵向动态影响最小的最佳轮胎力量分布是什么？鉴于轮胎力量高度非线性及与控制目标相比（横摆力矩、减速），车辆拥有多个执行机构（四个制动力），为了调节系统，可能存在一个以上的执行机构调整值，所以这个问题的答案极具挑战性。状态相关黎卡提方程是优化调节非线性过度执行系统的合适技术方法。1992年，Krikelis等人对状态相关黎卡提方程控制了一些首批研究，而更加系统化的发展是在1996年由Cloutier等人开展的。

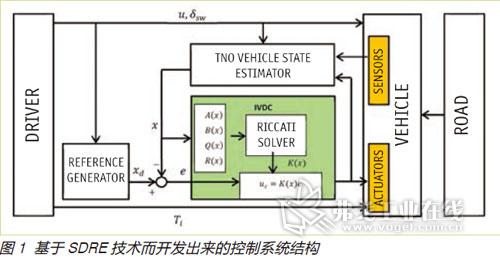
图1所示为所开发的以状态相关黎卡提方程技术方法为基础的控制系统结构。使用基准模型的基准发电机和乘驾人员输入（即转向轮角δsw和纵向速度u ）提供了车辆的理想状态xd。TNO车辆状态估算器（VSE）估算出在当前运行点上车辆的状态x。e（理想状态和估算状态间的误差）是综合车辆动态控制（IVDC）的输入。综合车辆动态控制（IVDC）模块包括以综合滑移TNO MF-Tyre模型为基础的系统状态空间方程非线性方案、控制的目标，控制目标是以数学成本函数和状态相关黎卡提方程数字解算器形式表现出来的最小轮胎纵向滑移和滑移角。

非线性车辆模型是采用三状态模型（即纵向速度u、侧向速度v和摇摆速度r）产生的。在模型里，纵向、侧向和横摆方向的加速度是相应方向上轮胎力量的非线性函数。通过计算轮胎正常力时对负载传输的考虑，滚动动态对车辆行为的影响被包含进来，见公式（1）～（３）。

u˙ = vr + f（Fxi， Fyi） （1）

v˙ = -ur + g（Fxi， Fyi） （2）

r˙ = q（Fxi， Fyi） （3）

MF-Tyre综合滑移轮胎模型被用于描述各种轮胎力量行为 （Pacejka 2002）。使用这样一个轮胎模型有两个主要原因。首先，其大幅度地改善g机动状态下的车辆模型精确度。其次，为了计算最佳制动力分布，有必要考虑纵向和侧向力之间的互动性（Van Zanten， 1998）。

在状态相关黎卡提方程中，需要将非线性动态方程转换成类似线性的形式，称之为“状态相关系数（SDC）公式”，见公式（4）。

x˙ = A（x）x + B（x）uc （4）

式中，x 是车辆状态[u，v，r]T。

在将方程（1）转换成SDC形式时，较大的困难是综合滑移轮胎行为。为了避免这种困难，多数研究人员都执行解耦轮胎模型（Bonsen， 2010）。建议采用下列表达式表示使用MF-Tyre模型的综合滑移轮胎行为：

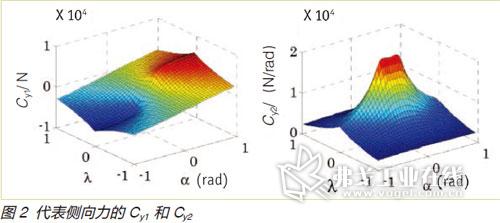
Fx = Cx1（λ，α）λ+Cx2（λ，α）α（５）

Fy = Cy1（λ，α）λ+Cy2（λ，α）α（６）

状态相关黎卡提方程理论还容许将约束值增加到执行机构上（如执行机构饱和）。控制系统uc的输入涉及到车轮的纵向滑移，这种滑移可以是正面的，也可以是负面的。约束值被认为可防止正面滑移或加速。

设计的SDRE控制使成本函数实现最小化，

J = ∫（xTQ（x）x + uTC R（x）uc）dt （7）

式中，Q（x） 和 R（x）是状态和输入权重矩阵，而且一般与状态相关。

优化相对于约束值的成本函数的状态反馈定律是：

uc = –K（x）x （8）

式中，K（x）是状态反馈增益，

K（x） = R（x）–1B（x）TP（x） （9）

而P（x）是代数状态相关黎卡提方程的解。

A（x） TP（x） + P（x）A（x） – P（x）B（x）（10）

R（x）–1B（x） TP（x） + Q（x） = 0 （11）

实时解决代数黎卡提方程有几种数字方法。为了防止实时处理器过负载，采用迭代最佳次数，对克莱曼算法进行了修改。

在一间乘驾汽车实验室里，通过在实时dSpace平台（dSpace Autobox 1005）上实施拟议的控制方略，从而对其进行试验性评估。CarLab是一款捷豹XF汽车，装备有线控制制动系统和标准ESC传感器组。在CarLab上，还执行了TNO的车辆状态估算器（VSE），给SDRE控制器提供全面的状态反馈。另外，通过将使用拟议中的控制器所获得的试验结果（表示为TNO IVDC ）与使用解耦滑移轮胎模型（表示为基准）（Bonsen，2010）所获得的结果进行比较，就非线性综合滑移轮胎模型对最佳轮胎力量分布的情况进行了调查。

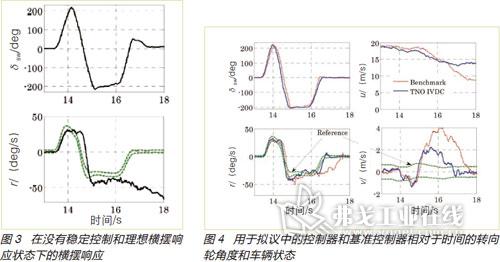
在试车跑道上进行了几次试验后，但是出于简便的目的，在此仅只显示正弦停滞机动性的情况。据NHTSA称，这项性能试验是激发宽范围车辆转向过度响应的最好方法。在正弦停滞测试中，车辆起初以75km/h的速度向前直行。然后，在某个时间点上，转向轮开始移动，在第二个尖峰开始时，δsw跟随0.7Hz正弦波，有500ms的滞后（见图3上半部分）。图3下半部分显示了在没有稳定控制状态下，CarLab的横摆响应和理想横摆响应，犹如所观察到的情况那样，在机动性被起动后1.2s，横摆速率开始偏离，甚至当转向轮回正时，机动性也尚未回到零点，这意味着车辆变得不稳定。

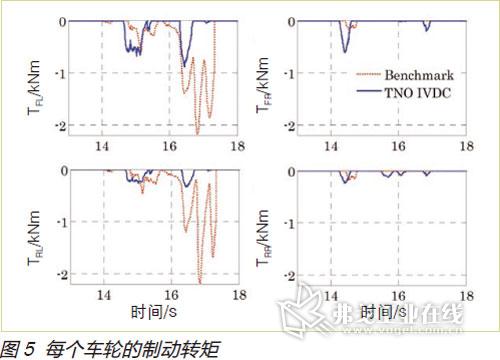
图4所示为拟议控制器和基准控制器与时间相关的转向轮角度和车辆状态（[u，v，r]T）。测试结果发现，两种控制器改进后都提高了车辆稳定性。因此，二者都满足IVDC的第一个目标。但在车辆的横摆速率和侧向速度响应方面（侧向速度降低了0.12km/h），拟议中的控制器展示出更好的性能。此外，与基准控制器相比，它对纵向速度的影响也较小，因此，表现出在IVDC的第二个目标方面也有改进。可以看出，在机动性结束时，装备拟议控制器的CarLab速度下降了15km/h。图5所示为每个车轮的制动转矩，所提到的两种控制器的制动力分布截然不同。就横摆速率响应（见图4）在13～15s的情况而论，虽然车辆转向过度，但是基准控制器对前后轮施加同样的转矩，而拟议控制器对后轮施加的转矩要小一些。从15～16.5 s之间，配备拟议控制器的车辆转向不足。因此，控制器在前轮上施加更大的制动转矩，拟议中的SDRE技术方法更适合最佳制动力分布。

调查表明，在各种机动性状态下，拟议中的SDRE控制器有能力稳定车辆，并具有最佳制动力分布。与基准控制器相比，一方面控制器改善了车辆性能，而同时又将侧向速度保持在0.12km/s以内；另外一方面将干预保持在最小限度内，速度下降不到15km/h。

对于配备综合滑移轮胎模型的车辆，拟议中的SDC形式提供恰当框架，包括更多执行机构。将来，TNO属下的车辆安全局将研究IVDC中主动悬架系统和乘驾舒适性目标与成本函数间的关系。