基于多目标规划优化设计理论，本文探讨了在多目标制约的条件下圆柱螺旋弹簧的最优化设计，以获得弹簧最佳的设计尺寸参数，并利用MATLAB GUI开发了圆柱螺旋弹簧的优化设计软件，保证了弹簧零部件的设计精度及开发效率。

随着汽车工业的发展，汽车的零部件设计也在不断改进和完善。特别是作为支撑部件的螺旋弹簧，除了满足设计的刚度、强度和空间间隙等要求，对弹簧设计的轻量化以及设计的高效率也提出了新的要求。传统的汽车螺旋弹簧在设计时难以得到最佳的设计方案，而且对设计师的能力提出了较高的要求，资历较浅的设计师很难胜任。为了克服上述缺点，利用电子计算机按最优化数学方法对螺旋弹簧进行优化设计是较好的解决办法。

通过建立圆柱螺旋弹簧的质量最小作为优化目标，利用随机搜索和迭代的优化理论进行优化。该方法目标比较单一，优化的结果受到设计变量的初始值以及约束范围的影响较大，优化效果不佳。以弹簧的重量最小、刚度和应力最大为优化目标，利用遗传算法进行优化对于定目标刚度的优化结果不适用。为了取得良好的优化效果，同时保证螺旋弹簧的动力特性，本文以弹簧质量最轻以及刚度与目标最接近作为优化目标，建立多目标规划的数学模型，用评价函数法进行求解，最终得到满足设计需要的最优解。

多目标规划问题

1. 数学模型

多目标规划问题与非线性规划问题的主要区别在于，它所追求的目标不止一个，而是共同作用的多个。其形式可以表达如下：

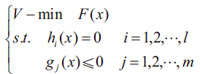
其中，设计变量；目标  令

则称R为问题的可行域，V-min F(x)指的是对向量形式的p个目标函数求最小。

2. 多目标规划问题的处理方法

首先求解p个单目标规划问题：

令各问题的最优解为 数字4，而其目标函数值可以表示为：

利用各目标优化函数值构造最短距离理想点法的单目标规划问题的评价函数，以评价目标函数到理想点间的距离，并使得目标函数与理想点之间的“距离”尽可能小，其形式表达如下：

圆柱螺旋弹簧的优化设计

1. 设计变量

取螺旋弹簧的簧丝之间d，弹簧中径D和有效工作圈数n作为优化设计的控制变量，即：

2. 优化目标函数

圆柱螺旋弹簧优化的目标函数应能最大限度地反映该弹簧的设计和使用要求，尽可能地提高材料的利用率，以及保证弹簧本身的动力特性。因此，在保证所设计刚度与目标刚度误差最小化，并尽可能减轻弹簧重量的情况下，将目标函数分别设计为：

式（1）、（2）分别为重量最小，刚度最接近目标。

3. 设计的边界条件

根据对弹簧功能和结构的要求，列出弹簧设计的约束方程。约束方程包括最大允许的材料应力、疲劳强度安全系数、要求的弹簧高径比、剩余有效间隙约束以及弹簧旋绕比和共振等，具体见以下方程式：

式中：P为弹簧收到的最大工作载荷；K为弹簧曲度系数

；C为旋绕指数， ；S为疲劳安全系数；Smin为最小安全系数，取Smin=1.2；C为弹簧高径比；ƒ r为弹簧自振频率，为了避免共振，一般限制其自振频率大于工作频率的5~10倍；

4. 设计变量的约束范围

设计变量约束，按照车辆设计要求，给出丝径d、中径D、有效圈数n的约束范围，即定义如下：

5. 优化函数的计算处理

由以上所建立的优化模型可知，该多目标规划问题是一个双目标，具有三维7个不等式约束优化问题。根据模型特点利用MATLAB自带的优化工具fmincon优化函数进行分析。

按照多目标规划问题的处理方法编写目标函数objfun1和objfun2，利用MATLAB自带非线性优化工具箱fmincon把各子目标在相同的不等式约束条件gi（x）≤0，（i=1,2,…,m）下分别单独进行优化：

[x1,f1]=fmincon（@objfun1,x0,[],[],[],[],[],[],@confun）；

[x2,f2]=fmincon（@objfun2,x0,[],[],[],[],[],[],@confun）；

其中，confun是约束条件的程序文件。最后将上述优化所得的各目标函数值f1、f2构造出新的向量，并以为理想点，利用式（5）构造出多目标的评价函数：

在相同的约束条件confun下进行优化，得到最优的[d,D,n]解。

多目标优化设计的程序及GUI界面实现

利用MATLAB/GUI良好的用户界面功能完成螺旋弹簧优化设计主界面的编制工作，编制按以下流程进行（见图1）。

最终完成的螺旋弹簧优化设计用户使用界面如图2所示。

应用实例

已知某车辆弹簧，安装空间最大允许150mm（即式（15）中的Dupp=150），安装高度Hc=198.64mm，最大及最小弹簧长度分别设定为253.02mm和127.39mm，初始载荷Fc=3468.16N，最大工作载荷Fm=5249.31，规定目标刚度25N/mm，材料选用60Si2MnA，许用应力[τ]=920MPa，丝径和圈数范围可按式（15）规定，给定初始Xo=[x1,x2,x3]T=[10,1004]T。

在相同的约束条件下进行优化，得到最优的[d,D,n]解，优化结果如图3所示。

由表1可知，经过多目标优化后的弹簧参数更加符合实际工程需求，对材料的利用率更加充分，不但均衡了弹簧重量、弹簧刚度及应力，而且旋绕指数大稳定性更高，最大工作载荷下的剩余间隙更大有利于减小弹簧并圈相互碰撞的几率。

结束语

本文将多目标规划问题的优化方法与弹簧设计理论分析相结合，利用各目标优化函数值构造最短距离理想点法的单目标规划问题的评价函数，以评价目标函数到理想点间的距离，并使得目标函数与理想点之间的“距离”尽可能小，建立了圆柱螺旋弹簧优化设计的数学模型。利用MATLAB优化工具箱，实现了螺旋弹簧多目标优化。并基于MATLAB/GUI的界面功能，开发出该优化系统的界面程序，实现了圆柱螺旋弹簧的快速设计与开发，从而可以帮助设计人员有效地提高设计效率，缩短设计周期。该方法已经过开发车型的试验验证，取得了良好的使用效果，由此可知该优化设计方法具有较高的适用性及经济性。