为了进一步简化电动机转子的制造及装配工艺，使其更加适合高速应用场合，本文针对采用分数槽集中绕组方案的小功率永磁电动机，提出一种基于梯形永磁体的切向内置式新型转子结构。在定子采用分块铁心结构的基础上，对转子表面结构进行优化，详细分析了相关转子结构参数对电动机转矩脉动和平均转矩的影响规律，为该类电动机的设计提供了一定的参考价值。

1 电动机模型和参数

本文以一台10极12槽电动机为例，研究电动机转子结构参数对电动机性能的影响规律。电动机参数如表1所示。为了简化电动机转子的加工及装配工艺，提出的新型梯形永磁体切向内置式转子结构的永磁同步电动机的结构如图1所示。

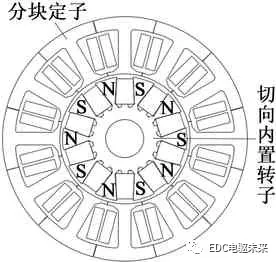
图1 电动机拓扑结构

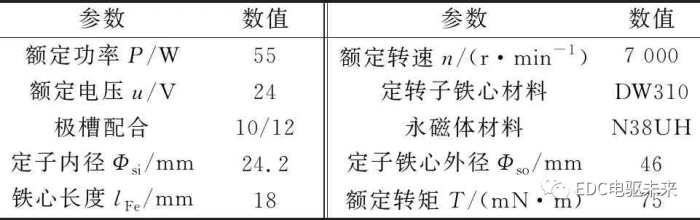
表1 10极12槽电动机主要参数

电动机采用分数槽集中绕组方案，电动机定子采用分块拼接的结构方式，可以方便地实现自动化嵌线工艺、降低生产及加工成本。转子采用切向内置式结构，梯形永磁体直接插入到转子槽中。相对于传统的切向式电动机转子，新型结构既降低了转子铁心的加工成本，同时也简化了转子的装配工艺。

2 切向式转子结构优化

对电动机转子结构的优化，分为永磁体结构参数和转子表面结构参数优化两个部分。永磁体结构参数包括下底边宽度l1、上底边宽度l2和高度，其中下底边宽度l1和高度可以根据电动机结构先行确定。电动机转子内径受电动机轴的限制，考虑到转子加工及装配要求，转子内圈厚度可基本确定。受到上述条件限制，永磁体的高度已经确定，不再作为优化参数。

2.1 确定永磁体下底边宽度

在不考虑饱和的情况下，转子中永磁体的体积与电动机转子的永磁磁链成正比，为了保证电动机转矩输出能力，在优化转子结构之前，首先要保证梯形永磁体的下底边宽度最大。而永磁体下底边宽度越大，转子铁心的连接桥宽度越小，从而影响了电动机转子的应力。本文确定永磁体下底边宽度的原则是保证电动机转子应力的前提下，连接桥宽度最小。确定梯形永磁体的下底边宽度后再通过有限元方法确定上底边的尺寸参数。

为了确保电动机转子结构的机械强度能满足电动机运行要求，本文采用有限元方法，建立转子结构的三维模型，施加电动机额定转速的旋转惯性载荷，对电动机转子的结构应力进行校核。图2为电动机转子应力分布云图。由图2中可以看到，转子铁心最大应力为0.98 MPa。电动机转子材料为硅钢片，其屈服强度为405 MPa，根据比较，该情况下转子所受最大应力小于其屈服强度，因此该转子结构满足机械要求。

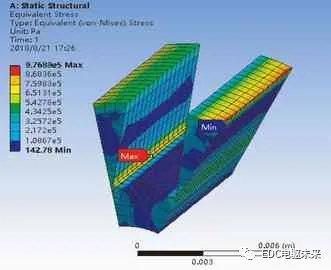
图2 转子平均应力分布云图

2.2 永磁体上底边宽度l2优化

通过有限元仿真软件，运用瞬态求解分析法，分别得到平均转矩、转矩脉动和齿槽转矩随上底边宽度参数的变化趋势。方便起见，引入系数λ=上底边宽度l2/下底边宽度l1，当λ=1时，即永磁体为矩形。

图3为λ变化时电动机的转矩性能仿真结果。从图3(a)可以看出，随着系数λ的增加，电动机平均转矩增大,齿槽转矩先较小后增大随后又减小，转矩脉动随之增大。由此可以看出，在确定永磁体尺寸时，应当在满足加工误差及装配工艺的前提下，综合考虑电动机输出转矩和转矩脉动的要求，从而确定λ的取值。根据以上分析综合考虑，本文λ取值为0.86。

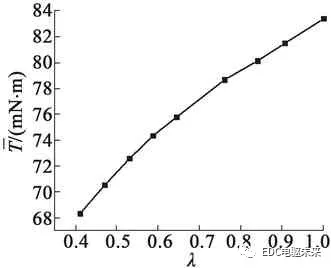
(a) 平均转矩随λ变化曲线

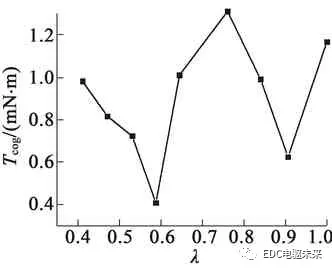
(b) 齿槽转矩随λ变化曲线

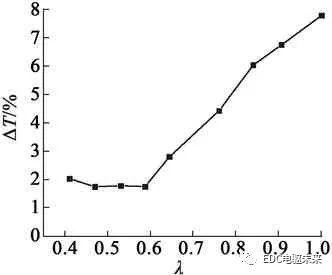
(c) 转矩脉动随λ变化曲线

图3 系数λ对电动机转矩的影响规律

2.3 转子表面结构优化

为了减小电动机转矩脉动，需要对电动机转子表面进一步优化。通过在转子表面开凸槽来改善气隙磁场和电动势波形，转子表面开凸槽电动机模型如图4(a)所示。图4(b)为转子外圆表面优化示意图，在优化后的转子外圆采用非等径结构，优化前与优化后的距离设为h，不同的优化参数h对气隙磁场、电动势波形和平均转矩、转矩脉动都会产生影响。

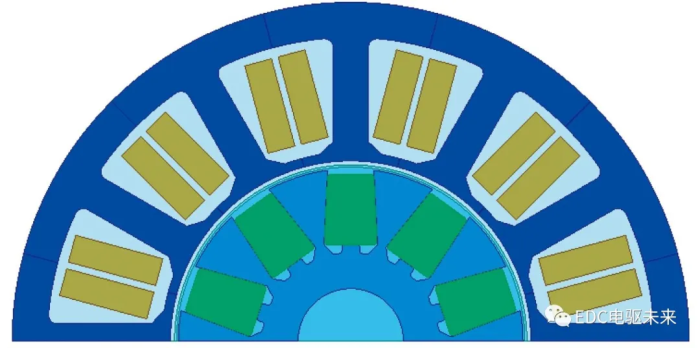
(a) 电动机结构图

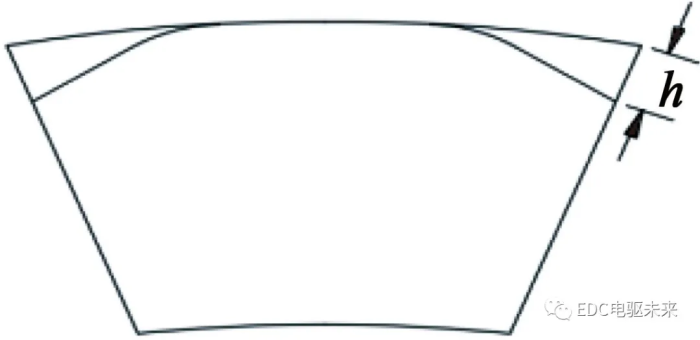
(b) 转子外圆表面优化示意图

图4 转子表面优化示意图

为了进一步研究转矩随h的变化规律，本文分别对平均转矩、齿槽转矩和转矩脉动进行仿真分析。图5为转矩随h的变化曲线。图5(a)为平均转矩随h变化曲线，平均转矩随着h的增大逐渐减小。图5(b)为齿槽转矩随h的变化曲线，随着h的增大齿槽转矩呈减小趋势，当h=0.2 mm时的齿槽转矩达到最小值。图5(c)为电动机转矩脉动随h的变化曲线，随着h的增大，电动机的转矩脉动先减小后增大，当h=0.3 mm时，转矩脉动达到最小，为5.9%。

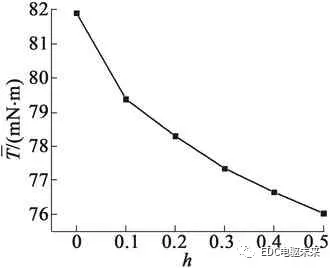
(a) 平均转矩随h变化曲线

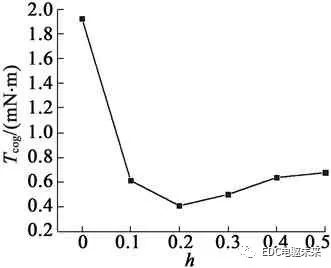
(b) 齿槽转矩随h变化曲线

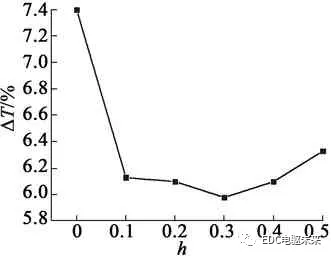
(c) 转矩脉动随h变化曲线

图5 转矩性能变化曲线

根据以上分析，对优化前转子h=0的结构和优化后转子h=0.2 mm的结构分别进行气隙磁密及空载反电动势分析。当h=0时，气隙磁密基波幅值为1.1 T，气隙磁密畸变率为11.93%；当h=0.2 mm结构时，气隙磁密基波幅值为1.08 T，气隙磁密畸变率为7.3%，与h=0相比，减小了4.63%。本文针对h=0.2 mm的电动机转子结构进行空载反电动势分析。图6(a)为优化前和优化后转子结构下空载反电动势波形图，图6(b)为空载反电动势的傅里叶分析。从图6中可以看出，h=0.2 mm空载反电动势的畸变率为11.3%，较h=0时的畸变率13.61%减小了2.3%， h=0.2 mm时的空载反电动势波形更加接近正弦。因此，通过在转子表面开凸槽可有效改善气隙磁场和反电动势波形。

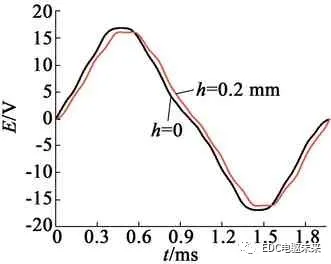
(a) 空载反电势波形

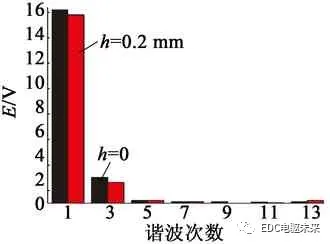
(b) 空载反电势傅里叶分析

图6 优化前后空载反电动势仿真对比

3 样机实验

切向内置式转子结构如图7所示。图8为样机实验平台。测试实验平台所使用的仪器设备包括：示波器、原动机电动机驱动控制系统、直流电源、实验样机、制动器等。通过控制器控制原动机的转速，由原动机带动样机旋转发电，示波器所检测得到的三相电压波形即为空载反电动势波形。

图7 转子及样机

图8 实验平台

样机的空载反电动势波形如图9所示。由实验结果可得，当电动机转速为2400r/min和6000r/min时，三相空载相反电动势幅值分别为4.78 V和12.00 V，同样工况下的仿真结果为4.99 V和12.49 V，误差为4%。主要是由于电动机各个部件的加工误差如定子、转子、永磁体及装配误差等原因导致。

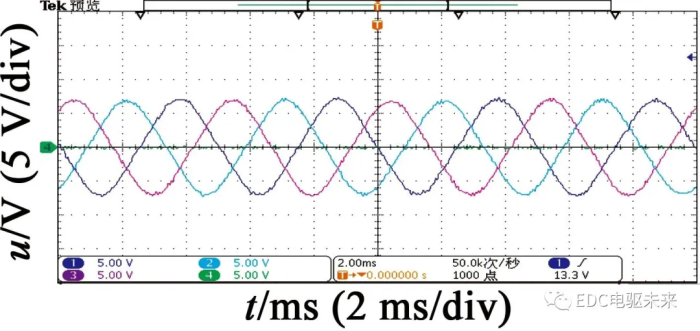
(a) 200 Hz下的反电动势波形

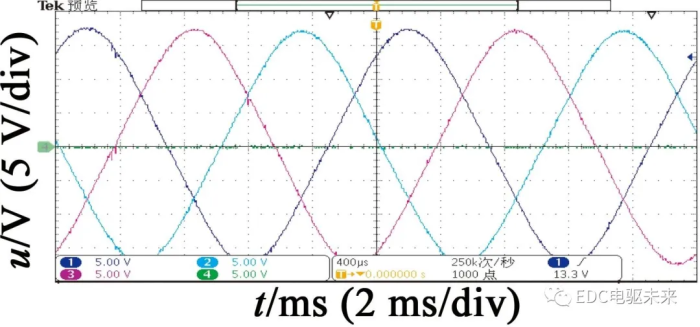
(b) 500 Hz下的反电动势波形

图9 空载反电动势实验波形

本文实验样机的转矩较小，由于实验环境和测试设备的限制，无法测得较精确的电动机转矩波形和转矩脉动。为了验证样机设计的正确性，本文进行了电动机额定负载下的转速测试。图10为电动机在额定负载情况下的转速测试曲线。由图10中可以看出，给定转速为±5 000 r/min及±7 000 r/min时，电动机能在额定负载下较好地跟踪转速给定值，转速平稳。

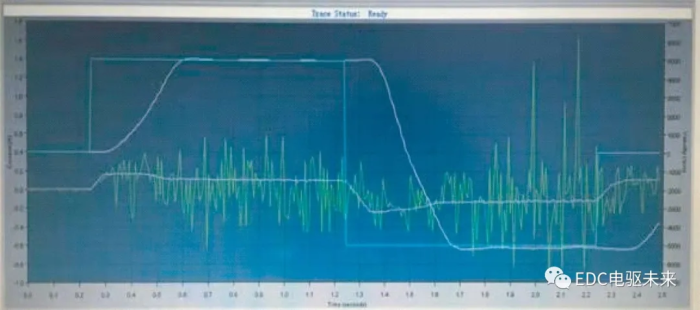
(a) 5 000 r/min转速响应曲线

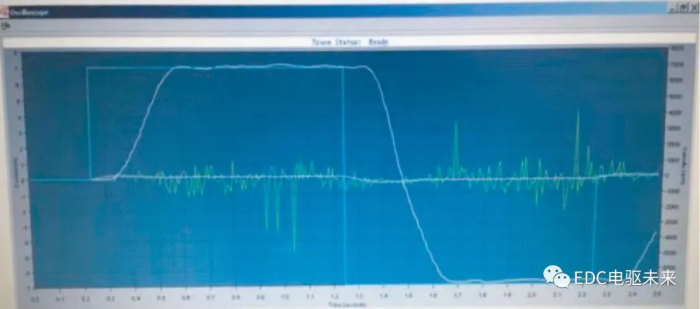
(b) 7 000 r/min转速响应曲线

图10 额定负载下电动机转速波形

4 结 语

本文针对高速小功率永磁电动机，为简化电动机生产工艺，提出了一种基于梯形永磁体的切向内置式转子结构。根据有限元仿真结果分析可知，在确定永磁体参数时，要综合考虑输出转矩、转矩脉动、加工工艺及误差的影响；并通过转子外表面优化可以进一步减小电动机的转矩脉动。研究结果表明，在转矩性能下降较小情况下，新型电动机转子结构可大幅简化转子工艺及成本，为该类型电动机的优化设计提供了一定的工程设计经验和参考。