本文中以一款新型双电机耦合系统电动汽车（dual-motor coupling-propulsion electric vehicle，DMCP-EV）为研究对象，制定了基于PSO算法系统效率优化的驱动模式控制策略，在满足动力性要求的基础上提高了整车经济性。

该款新型耦合驱动系统如图1所示。在该耦合驱动构型中，电机M1与太阳轮S相连，电机M2与连接器T相连。制动器L1与太阳轮S同轴，当L1闭合时，太阳轮被固定，电机M1停止运行。制动器L2与齿圈R相连，当L2闭合时，齿圈R固定。减速齿轮G1与齿圈R相连，当连接器T位于右端时，三者相连接，随电机M2的运转而运行；当连接器T位于中间时，电机M2关闭；当连接器T位于左端时，两电机转矩在太阳轮C处耦合。

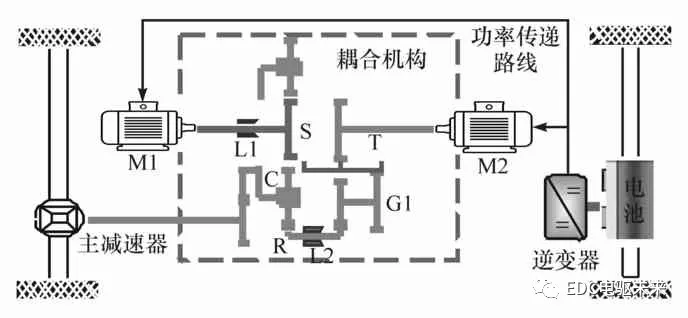
图1 新型双电机耦合系统构型

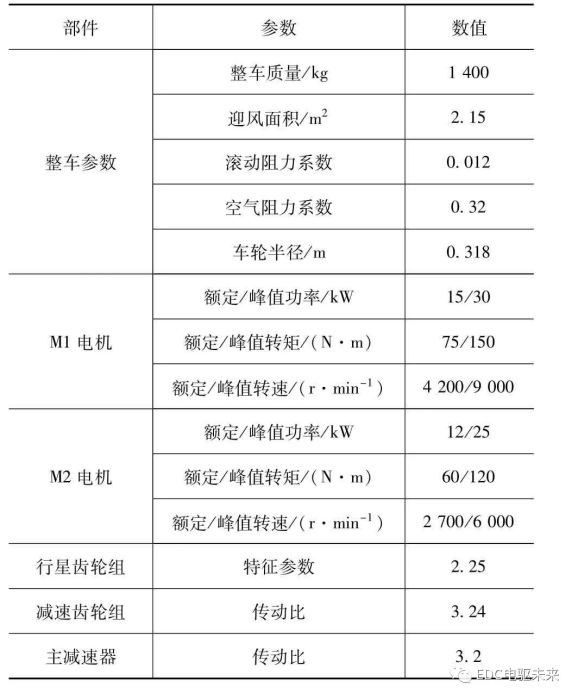
当汽车正常行驶时，整车控制器接受并处理来自传感器的信号，向电机控制器等执行器发出指令，通过控制连接器T及制动器L1、L2的开闭，使动力系统工作在不同的工作模式：电机M1单独驱动模式（定义为SM1）、电机M2单独驱动模式（定义为SM2）、双电机转矩耦合模式（定义为TC）、双电机转速耦合模式（定义为SC）以及再生制动模式。由于本文重点研究的是驱动系统的驱动性能，故在此暂不考虑再生制动的控制。本文中所研究的某款纯电动汽车的具体动力部件参数见表1。

表1 EV动力部件参数

1.2.1 工作模式分析

当制动器L1断开，L2闭合，且连接器T位于中间位置时，电机M1工作，M2关闭，系统处于电机M1单独驱动模式，则SM1系统动力学模型为

式中：n1为电机M1的转速；T1为电机M1的转矩；r为车轮半径；k为行星架特征参数；i0为主减速器传动比；F t为驱动力；v为车速。

当制动器L1闭合，L2松开且连接器T位于右端时，电机M1停止，M2运转，功率经减速齿轮、行星架输出。此时为电机M2单独运行模式，SM2模式系统动力学模型为

式中：i g为减速齿轮组的传动比；n2为电机M2的转速；T2为电机M2的转矩。

当制动器L1断开，L2闭合，且连接器T位于左端时，两个电机的转矩在太阳轮处耦合，经行星架传递到车轮，驱动汽车行驶。系统处于双电机转矩耦合模式TC，此时的系统动力学模型为

当制动器L1、L2断开，连接器T位于右端时，两电机转速在行星架处耦合，动力经行星架传递到车轮，驱动汽车行驶。系统处于双电机转速耦合模式，此时系统动力学模型可表示为

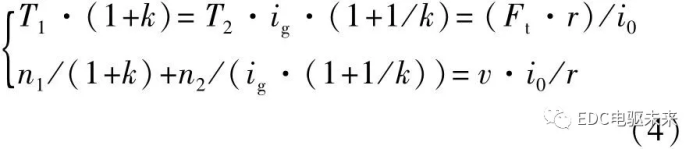
1.2.2 系统效率建模

不同模式下的系统效率数学模型为

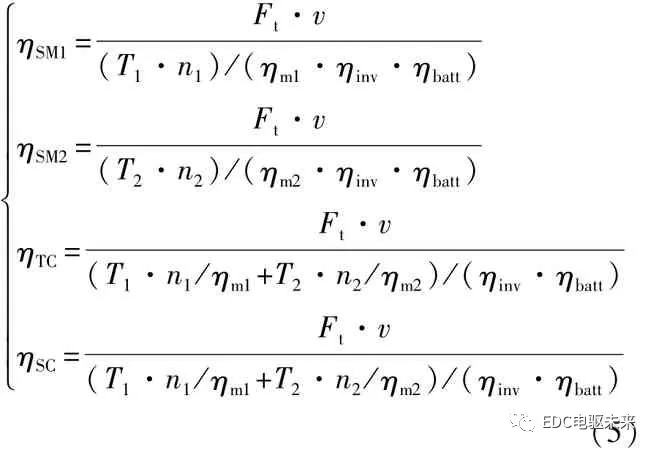
式中：ηSM1、ηSM2、ηTC、ηSC分别为 SM1、SM2、TC、SC模式下的系统效率；ηinv为逆变器效率。

约束条件为

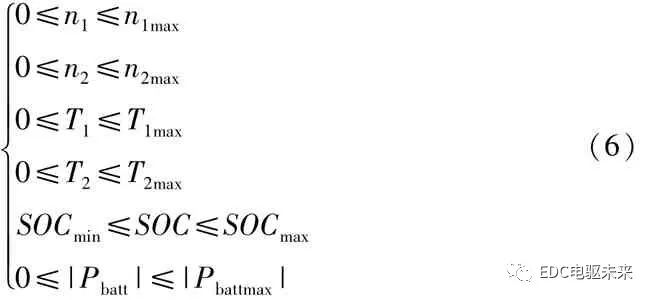
式中：n1max、n2max分别为电机 M1、M2的最大转速；SOC min为电池组最小荷电状态；SOC max为电池组最大荷电状态；P battmax为当前SOC对应的最大放电功率。

基于上述分析可知，DMCP-EV具有4种驱动模式。在动力需求的约束下，整车控制器根据获得的实时行驶速度、加速度信号、驱动电机的工作特性以及各个模式的工作原理，获得各个模式的工作范围。对各个模式工作范围的划分流程如图2所示，可简述如下，首先由车载传感器采集到速度、加速度信号，然后根据各个模式的动力学模型以及速度等信息，计算各个模式在该工况下所需要的电机转矩、转速，则可以获得各个模式的有效工作范围，如图3所示。

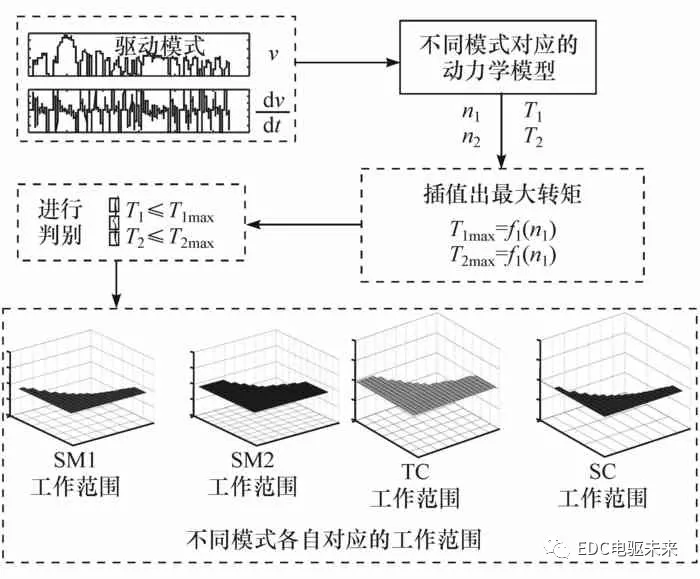
图2 不同模式工作范围划分流程

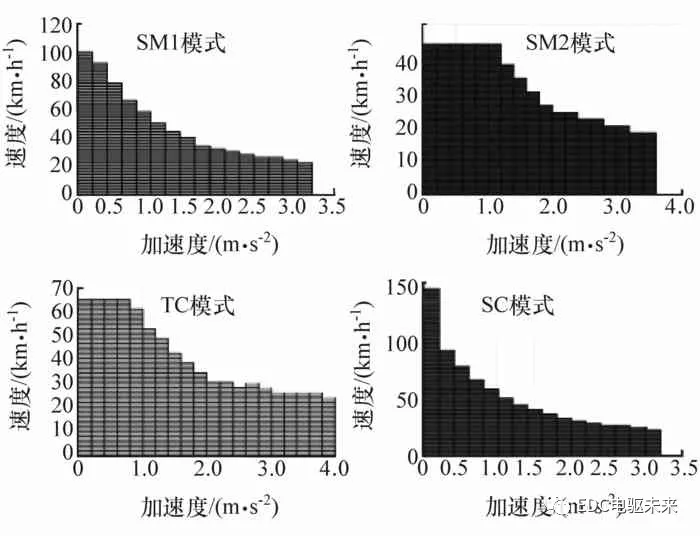
图3 不同模式下的有效工作范围

依据以上各模式工作范围的划分，满足当前速度、加速度以及驾驶员需求的工作模式可能有多种。为提高经济性，采用PSO优化各模式的系统效率，并根据当前行驶工况选择效率最优的工作模式。据此，本文中制定基于PSO系统效率优化的双电机耦合驱动系统控制策略，其框架如图4所示。控制策略是根据当前工况选择效率最优工作模式，具体步骤如下：

（1）判断满足当前工况的工作模式的情况；若仅有一个适合的模式，则选择该模式；若存在多个驱动模式，则进入系统效率优化控制模式；

（2）计算满足当前工况的各个工作模式系统效率，其具体计算过程详见1.2.2节；

（3）选择系统效率最高的工作模式作为当前工作模式以提高整车经济性。

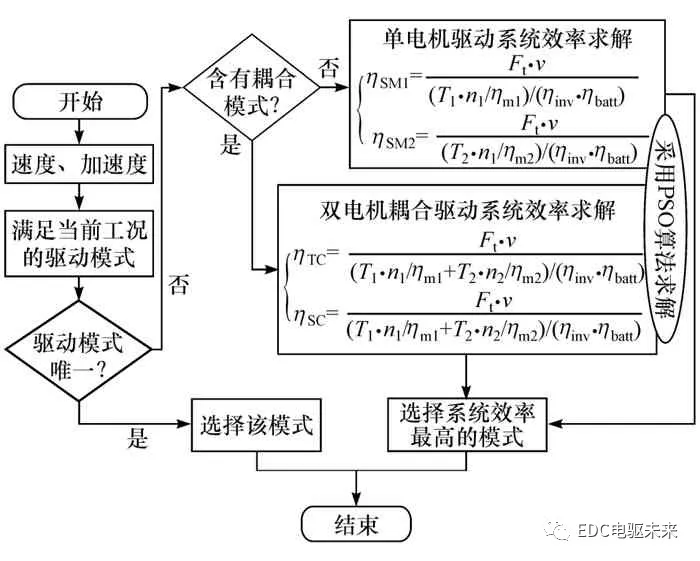
图4 基于粒子群算法的模式划分及控制流程

2.2.1 TC模式下的系统效率优化

TC模式下，两电机的转速与车速成比例，两电机的转矩相耦合，可以在约束范围内进行调节。采用粒子群优化算法优化两电机的转矩分配，以获得系统最优效率。PSO算法初始参数和系统效率流程如图5所示。TC模式系统效率优化过程为：给定速度和加速度，通过粒子群优化算法获得电机M1、M2的目标转矩，使系统效率ηTC达到最优。优化模型如下。

目标函数（适应度函数）：

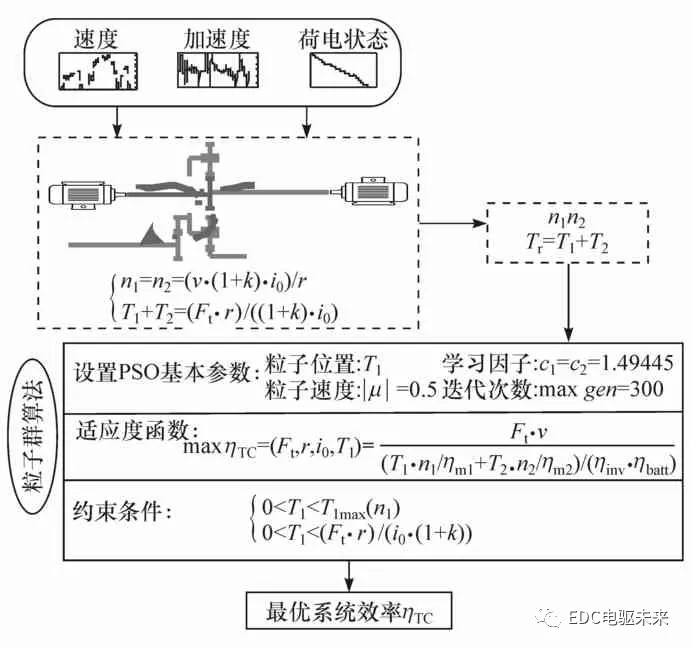
图5 粒子群算法优化系统效率流程图

约束条件：

选取M1电机的转矩T1作为控制变量，则其相应粒子的位置为

式中：i为粒子编号；j为迭代次数。

系统效率寻优结果如图6所示。由图可以看出，系统效率在第40代左右收敛至最优值。TC模式下的最优转矩分配如图7所示。

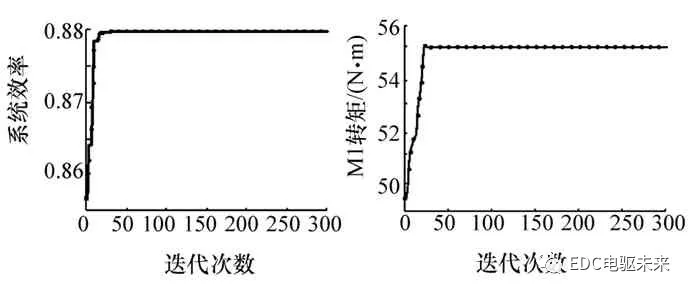
图6 PSO算法寻优迭代图

2.2.2 基于系统效率优化的模式控制

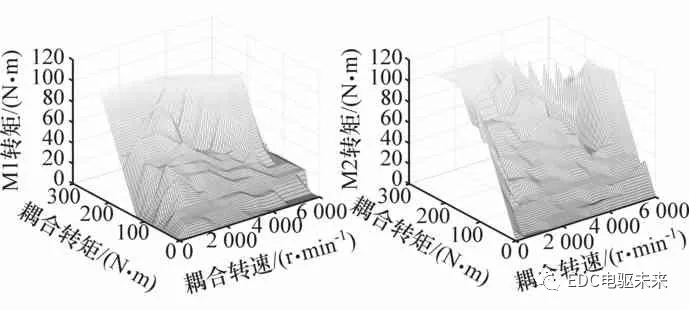
图7 TC模式下的最优转矩分配

在SC模式下，两电机的转矩与驱动力矩成比例，两电机的转速相耦合，可以在约束范围内调节。与TC模式类似，SC模式获取最优系统效率关键是合理分配两电机的转速。同样采用粒子群算法优化，具体求解过程与TC模式类似。图8为SOC＝0.9时优化后不同模式下的系统效率。适合当前工况的最佳驱动模式可通过比较该工况下4种驱动模式的系统效率而得出，即可以获得4个工作模式的工作边界，如图9（a）所示。为减少计算量并提高整车控制器工作效率，提前划分了各个工作模式的工作边界，如图9（b）所示。并将结果制成表格存储在控制器中，通过查表获得当前最优工作模式。

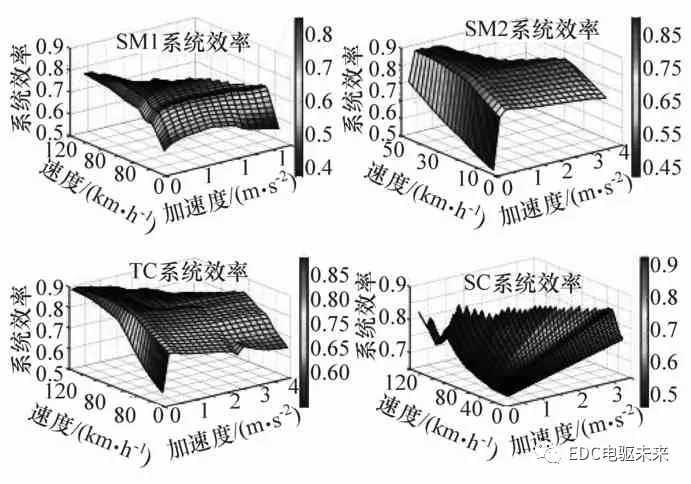
图8 SOC为0.9时不同模式下的系统最优效率

在Matlab／Simulink环境下实现装备该新型双电机耦合驱动系统的整车模型的搭建，通过优化前后结果对比来验证所提出的基于PSO系统效率优化的模式划分及选择策略的有效性。为体现对比结果的公正性，未经PSO效率优化的系统的模式划分方法与本文相同，模式的选择同样基于瞬时最优的原则，该模式选择策略分别实时计算当前工况下4种工作模式的需求功率，选取需求功率最小的模式作为当前工况下的工作模式。两者在城市道路循环UDDS下进行仿真，结果如图10（a）所示。由图可见，在整个工况过程中，实际车速很好地跟随目标车速。驱动时，该系统基于所提出的控制策略，自动匹配适合当前工况的工作模式，从而在满足车辆动力性能需求的同时，保证了较低的能耗。图10（b）和图10（c）示出该系统优化前后的工作模式随UDDS工况切换的情况，“1～4”分别表示 SM1、SM2、TC、SC工作模式。

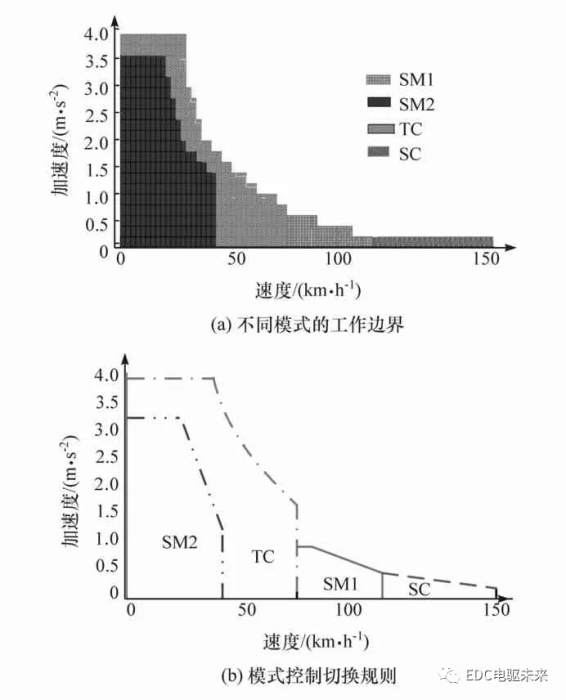
图9 不同模式的工作边界

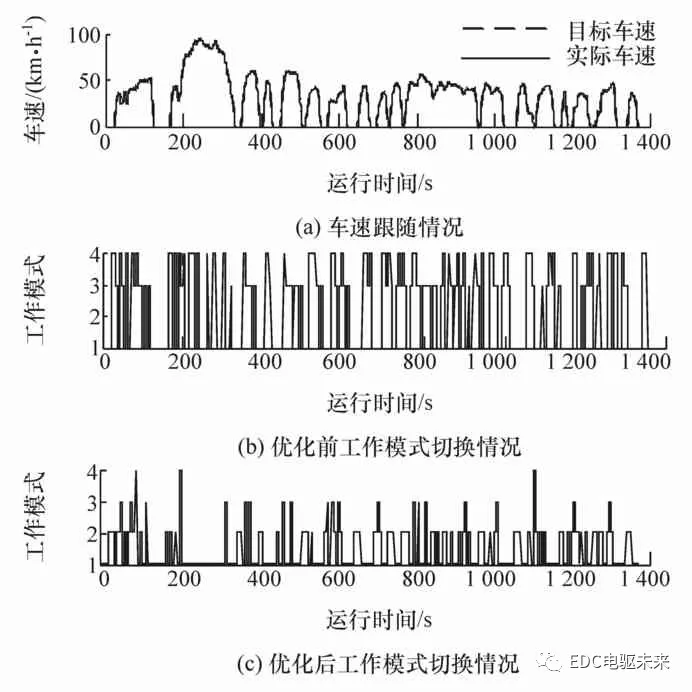
图10 车速跟随情况和优化前后的工作模式切换情况

图11给出了该系统PSO优化前后的两电机的转矩和转速。可以看出，优化前后的M1、M2电机转矩和转速分配变化明显。图12为优化前后的电机转矩以及转速的对比。可以看出，经优化重新分配转矩转速后，该系统的SOC变化范围缩小，能耗从优化前的1.165降低为1.036 kW·h，降低了11%左右，达到了提高整车能量经济性的目的。

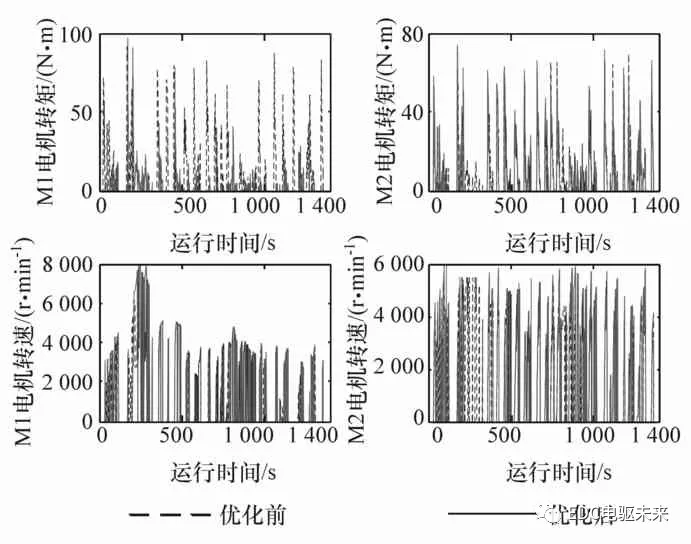
图11 优化前后的M1、M2电机转矩转速对比

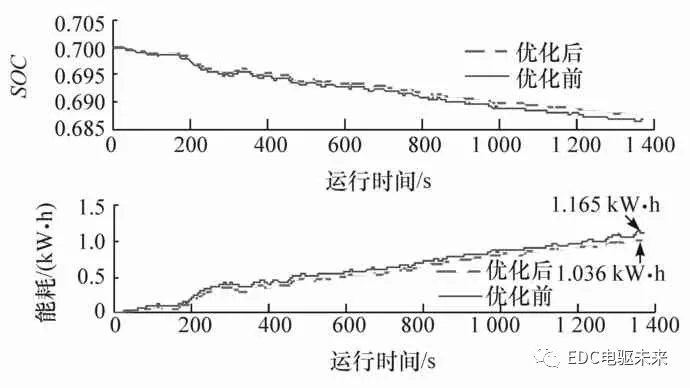
图12 优化前后的SOC和能耗对比

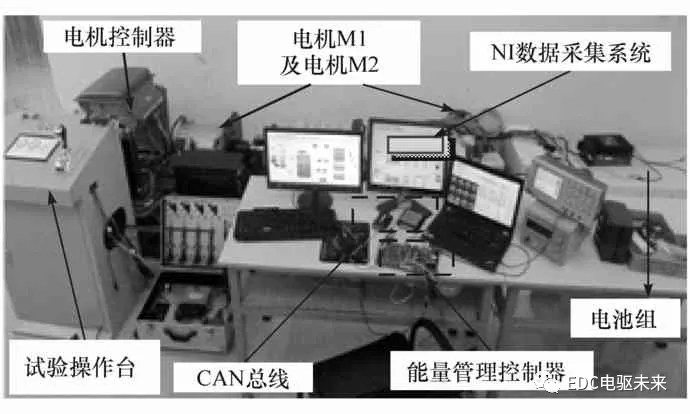
图13 台架试验实物图

为验证PSO系统效率优化的实际效果，基于双电机耦合驱动系统试验平台（图13）进行台架试验。选用飞思卡尔MC9S12EQ512汽车级微处理器作为该试验平台的主控制器主芯片。采用CAN总线进行数据通信，波特率设为250 kbps，采用J1939应用协议。使用LabVIEW软件设计上位机数据采集系统的软件部分，硬件部分由PXI数据采集卡、传感器和计算机组成。

试验分别以UDDS和EUDC循环工况进行验证。测得速度、系统效率和电池SOC的曲线图，并与仿真结果进行对比，结果如图14所示。可以看出，台架试验与仿真结果趋势基本一致。

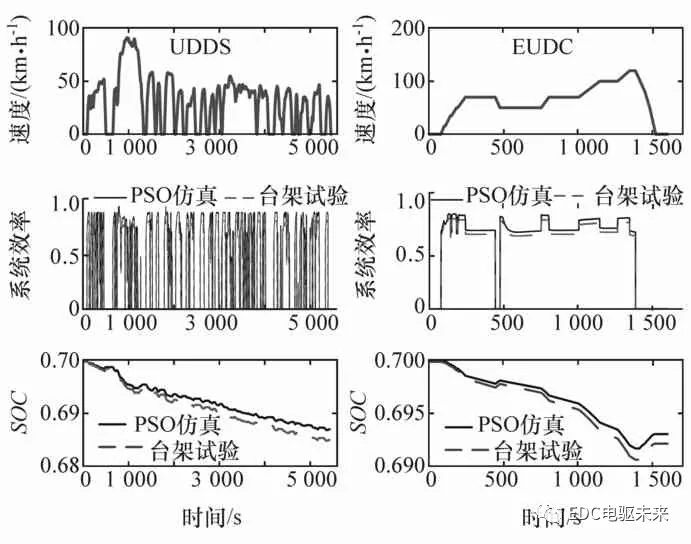
图14 UDDS和EUDC工况下的台架试验与仿真结果对比

综合上述的仿真和台架试验验证的结果，表明所制定的基于PSO系统效率优化后的DMCP-EV驱动模式控制能够有效改善双电机驱动系统的驱动效率，从而降低了能耗，提升了整车经济性。

（1）针对一款新型双电机耦合驱动系统及其多模式驱动特性，建立双电机驱动系统动力学和系统效率模型，并制定了经PSO系统效率优化的驱动模式控制策略。

（2）通过仿真和台架试验验证的结果表明，针对DMCP-EV所制定的经PSO系统效率优化的驱动模式控制策略，可获得更合适的驱动模式，提升双电机驱动系统的驱动效率，从而进一步提高DMCP-EV的经济性，优化后能耗降低11%。