随着汽车技术的飞速发展，大家对驾驶舒适性的要求也越来越高，转向系统作为驾驶员操控车辆的直接部件，对驾驶员的影响不言而喻。一般在转向系统设计时都会考虑方向盘中间位置的力矩波动幅值，往往会忽略方向盘调节全行程范围内的力矩波动变化趋势以及左右对称性。本文通过对转向系统双十字轴万向节建立动态模型，通过调整相位角以及节叉初始位置，总结出一种方向盘全行程的转向系统力矩波动优化方法，为设计提供依据。

转向系统力矩波动分析

转向系统是把驾驶员作用在方向盘上的力矩按照一定的传动比放大并传递到车轮实现车辆转向的增力装置，主要包括转向盘、转向管柱、转向中间轴及转向器等零部件（图1）。

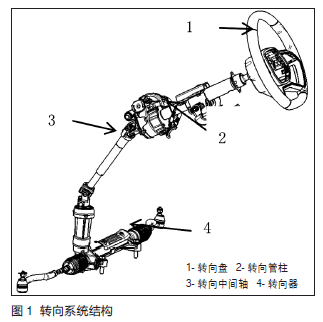
转向中间轴一般为双十字轴式万向节结构，上面十字轴连接转向管柱，下面十字轴连接转向器。转向中间轴力矩波动原理如图2 所示。由于十字轴式万向节的不等速特性，力矩传递过程中存在波动，影响驾驶员的手感，各主机厂一般会在整车硬点布置时尽可能使两个万向节的轴交角相等或接近（β 12=β 23），且两内节叉的相位角（耳孔轴线夹角）与平面角γ1 相等，以保证设计状态力矩波动最小。

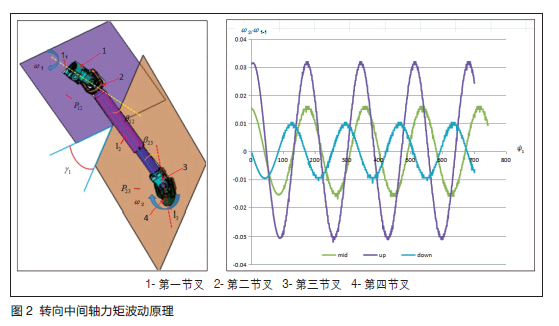
目前大多数转向管柱都具有角度调节功能以适应不同身高的客户群体，当角度调节后，硬点位置发生改变，力矩波动将会变化。当方向盘处于角度调节的不同位置时，力矩波动的变化趋势不同，影响驾驶手感。

理想的设计状态为，转向盘处于角度调节的任何位置时，力矩波动均处于波峰，驾驶员的操纵手力左右对称，且此时下轴旋转角速度比方向盘旋转角速度大，转向特性灵敏度最好。

建立转向系统力矩波动优化模型

以某车型转向系统为例，其硬点数据见表1。

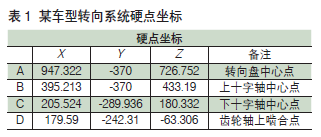
1. 建立硬点坐标模型

（1）创建旋转轴线模型(part)

创建下安装点旋转轴线、两端点坐标、轴线中点坐标以及过中点与轴线垂直的平面1。

（2） 创建基准硬点模型（part）

硬点坐标模型如图3 所示：①输入A 、B 、C 和D 点硬点坐标；②做A 、B 点绕旋转轴线旋转命令（旋转角度为上下调节角度，如±1.5°），得到A ′、B ′ 点；③ 创建直线A ′B ′、直线B ′C、直线CD ，以及平面A ′ B ′ C、平面B ′ CD ；④通过B′点分别创建垂直于直线A ′B ′、直线B ′C 的平面01、平面02 ；⑤ 通过C 点分别创建垂直于直线B ′C、直线CD 的平面03、平面04 ；⑥通过B ′点创建垂直于平面A ′B ′C 的直线B 1B 2，通过C 点创建垂直于平面B ′CD 的直线C1C2 ；⑦通过B ′点创建直线B 1′B 2′，以平面02 作为支持面，与直线B 1B 2 成一定角度（如90°）；⑧通过C 点创建直线C1′C2′，以平面03作为支持面，与直线C1C2 成一定角度（如90°）。

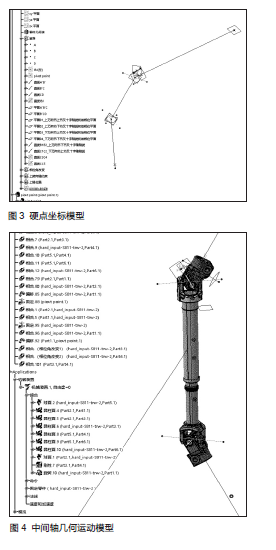
2. 建立转向中间轴几何运动模型

（1） 将中间轴分为6 个part，分别导入总模型装配体；第一节叉、第二节叉带套管、第三节叉带轴、第四节叉、上十字轴、下十字轴等共6 个part。

（2）创建几何约束中间轴几何运动模型如图4所示。先使基准硬点模型处于中间位置，即1.2-b 旋转角度为0，按照实车状态约束模型（备注：在第一节叉上做一个平面，与1.1中平面1 平行，此约束是防止上下调节时，节叉1 发生转动）；切换到DMU 界面， 创建DMU模型。

3. 改变相位角—模型自动变换重组

改变1.2-b 旋转角度后更新约束，即可以得到方向盘上下调节极限位置的转向系统模型；改变1.2-g 和1.2-h 的角度，并将直线B 1′B 2′与第二节叉耳孔相合，直线C1′C2′与第三节叉耳孔相合, 然后更新约束，即可以改变模型的相位角。

4. 设计状态（角度调节中间位置）节叉初始位置

（1）相位角等于（或接近）平面角时，第二节叉的耳孔轴线与平面A ′B ′C 平行时，力矩波动处于波峰位置，但此时上下极限位置的力矩波动不一定在波峰附近，与硬点坐标有关。

（2） 如果中间位置的力矩波动幅值处于中间水平（例如中间1.5%，上极限3.2%，下极限1%），可以通过调整相位角（使中间位置的力矩波动幅值均小于上下极限位置，倒推出此时的相位角，如中间2.3%，上极限2.4%， 下极限3.4%）， 实现方向盘上中下三个位置的力矩波动均在波峰附近。

（3）ω 2/ω 1-1 与ψ 1 的曲线周期为180°，一个周期内有1个力矩波动的波峰，1 个力矩波动的波谷，2 个力矩波动为零的位置。

数据处理

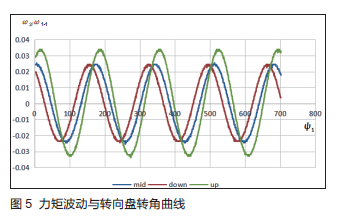
从DMU 界面激活传感器模块，导出ψ 1-ψ 2 数据，处理后得到ω 2/ω 1-1 与ψ 1 的曲线（图5，即为转向系统的力矩波动随方向盘转动角度的变化趋势。

总结

转向盘处于角度调节的任何位置时力矩波动均处于波峰，这是转向系统理想的设计状态。此时，驾驶员的操纵手力左右对称，下轴旋转角速度比方向盘旋转角速度大，转向特性灵敏度最好。受限于空间布置无法调整硬点时，也必须考虑转向转矩的左右对称性，并尽可能使任意位置的波动趋势一致。本文通过对转向系统双十字轴万向节建立动态模型，通过调整相位角以及节叉初始位置，总结出一种转向盘全行程的转向系统力矩波动优化方法，为设计提供依据。