该款混合动力专用变速箱是采用WW型简单行星排为耦合机构的双电机无级变速系统，主要由台阶式无齿圈行星排总成、发电机、电动机、减速齿轮、差速器、单向离合器、双机械油泵等组成。其中太阳轮1（S1）连接发电机（ISG电机），太阳轮2（S2）连接发动机，行星架作为输出端连接着驱动动机（TM电机），结构示意图见图1。

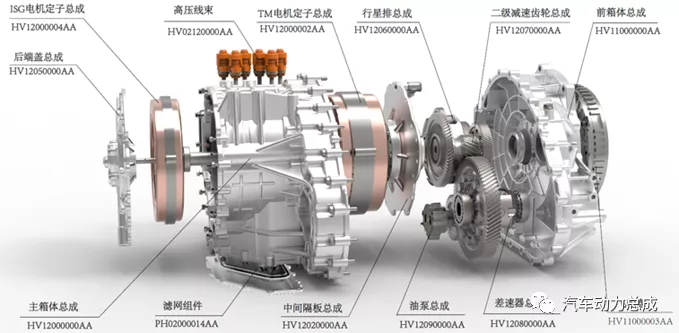
图1 DHT结构示意图

该动力耦合机构属于输入动力分流结构，其特点是在低速高传动比的时候效率较高，类似于丰田THS系统。行星架相当于THS的齿圈，和输出端相连接，因此当车速一定时，行星架的转速就唯一确定，根据简单行星排的运动学方程，连接发电机的太阳轮S1和连接发动机的太阳轮S2，它们的转速可以自由匹配。这样发动机的转速就和车速解耦，而且能在一定区间内实现连续变动（无级变速）。

模拟杠杆作为行星排分析的有力工具，其直观性大大降低了行星排理解上的难度。模拟杠杆如图2所示，三根纵线代表两个太阳轮和行星架的转速，以行星架为基准，齿数越少，也即速比越大的杠杆离基准越远。当行星架固定时，s1和s2的转速方向相同，因而它们分布于行星架杠杆的同一侧。设S2到基准行星架的距离为1，S1到行星架的距离为k+1，k称为行星排的特性参数。

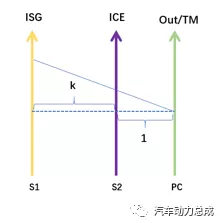
图2 DHT行星排等效杠杆

根据定义，行星排的特性参数可以看成行星架固定时的太阳轮到齿圈的速比，这里是两个太阳轮之间的转速之比。如图2，根据三角形相似原理，有

该箱行星排的运动学方程如下推导

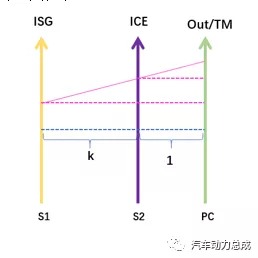
图3 转速特性示意图

如图3所示，根据三角形相似原理，有如下关系

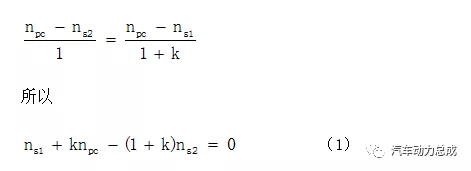
由公式1可见，与带齿圈的简单行星排比较，该行星排的行星架相当于简单行星排的齿圈，而行星排的大太阳轮S2相当于简单行星排的行星架。

根据杠杆平衡原理，在图3中，分别对s1和pc取矩得

由上述方程知，行星排内部受力中s1和pc的方向相同，与s2相反。

在式1中，小太阳轮s1有三种状态：1）转速为0；2）正转速；3）负转速。

定义行星排元件的转速和发动机相同时为正转速，反之为负转速。定义发动机转速和输出端转速之比为系统传动比，即

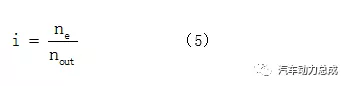
在无电池参与情况下，当小太阳轮s1转速为0时，电功率为0，发动机能量全部用于驱动车轮，系统效率最高。定义小太阳轮s1转速为0时的速比为机械点速比，即

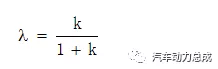
根据小太阳的状态，系统的电功率比例、输出效率也分三种情况讨论：

a）ns1=0,此时i=λ，如图4所示

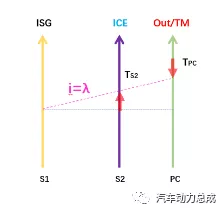
图4 机械点传动比杠杆

由行星排各轴扭矩平衡，可得如下方程

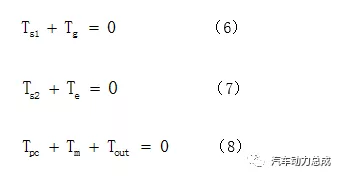
其中Ts1、Ts2、Tpc分别是小太阳轮、大太阳轮、行星架的扭矩，Tg、Tm、Te分别是发电机、驱动电机、发动机的扭矩，Tout是输出扭矩。因小太阳轮转速为0，所以电功率为0，即

Tg=0,Tm=0

联立上述方程，解得

当ns1＜0时，ISG电机功率大于0，为电动，TM电机功率小于0，为发电，假设系统运行过程中电池不参与，那么ISG电机的电能来自于TM电机的发电，于是根据电功率平衡得

发动机功率经过行星架后，一部分用于驱动TM电机发电，所以输出功率为

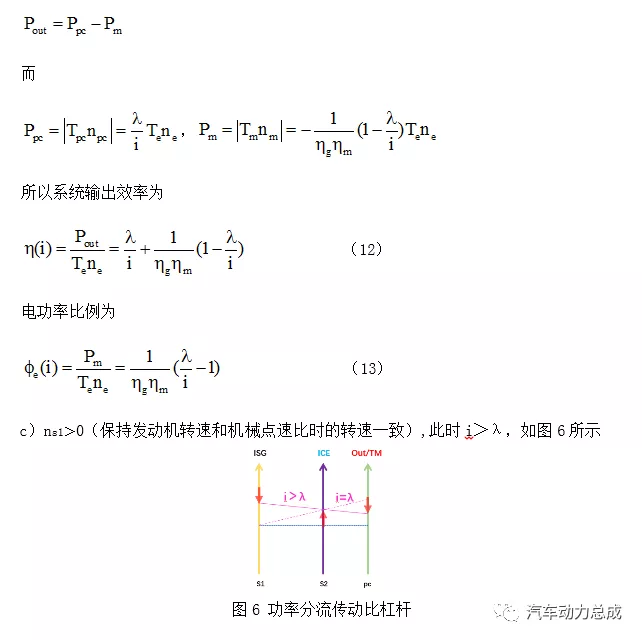
仿情形b)讨论，但此时电功率平衡方程为

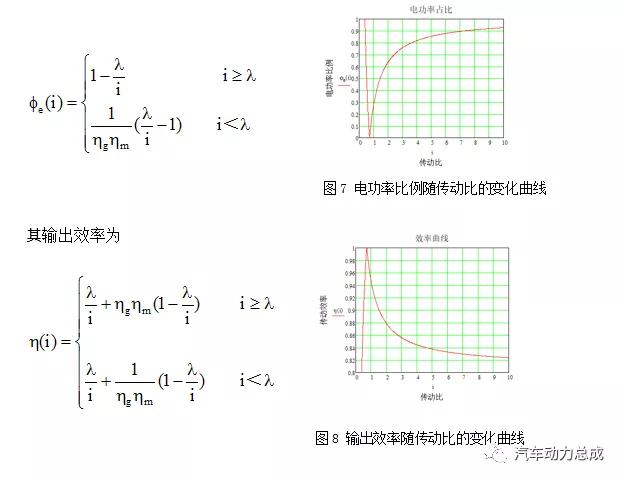
综合a)、b)、c)三种情况，行星排特性参数k取为2.65，两电机的发电或电动效率取为0.85，则该系统的电功率比例为

根据盖世汽车《新能源汽车电驱动产业报告（2021版）》预测，DHT将成为机电一体化的发展方向，混合专用变速箱DHT在系统集成度、重量以及综合能效方面的优势非常明显。

目前我司开发的该款DHT已经搭载样车，其动力性经济性的表现获得国内一众主机厂的广泛认可。

WW型行星排在动力系统中的应用并不多见，对其认识不够深入。本文结合实例试从该行星排的运动学、动力学以及能量方面对其展开讨论，抛砖引玉，以期更多同行参与讨论。