根据传热学原理，本文提出将轮毂电动机内部复杂结构的求解模型进行简化和等效处理，并通过相关流体力学的公式，计算出散热边界条件来模拟轮毂电动机的散热情况，最后将得出的轮毂电动机温度场的仿真数据与试验数据进行对比，验证了本文所提出的仿真计算方法的正确性，为轮毂电动机的冷却结构设计提供重要的理论依据。

轮毂电动机热性能参数的确定

1.轮毂电动机的基本参数

轮毂电动机的基本参数见表1。

表1 电动机基本参数

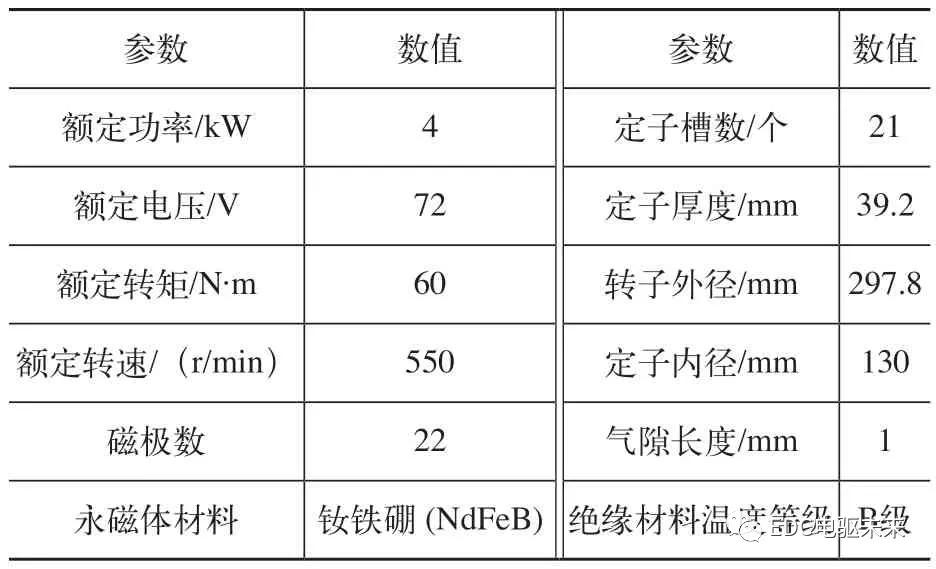
电动机内部结构较为复杂，结构较为紧凑，散热条件较差。在自然风冷条件下，轮毂电动机的主要热交换方式如图1所示，其中主要包括电动机内部各部件的传热、电动机外部壳体和内部结构的对流换热等组成。

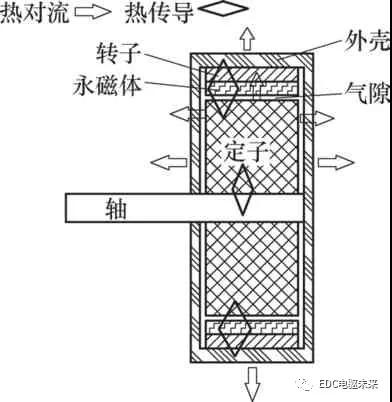
图1 电动机内热交换

2.热源计算

电磁损耗主要包括定转子铁心损耗、铜耗和永磁体涡流损耗，其中电磁损耗是轮毂电动机的主要热源，因此需要准确地计算出电磁损耗的具体数值。通过Maxwell电磁分析软件准确地分析出额定工况下轮毂电动机各部件的电磁损耗分布云图。如图2a所示，在齿顶处的定子铁心损耗较大，这是因为此处的磁密度较为集中。如图3所示，在齿槽开口处的永磁体涡流损耗较大，这是由于槽口存在的齿槽效应会产生磁场高次谐波，会引起较大的涡流损耗。

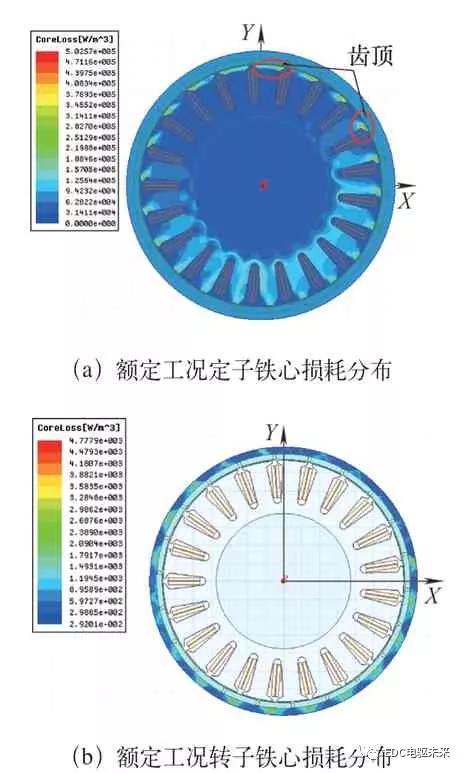
图2 额定工况定子和转子铁心损耗分布

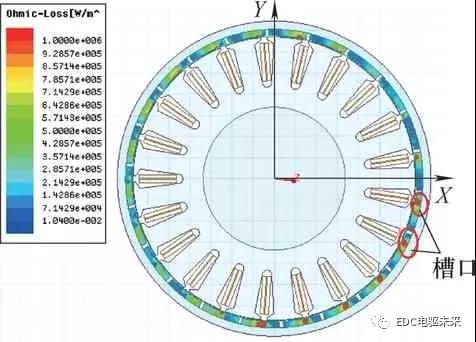
图3 额定工况永磁体涡流损耗分布

经过Maxwell后处理计算模块，得到轮毂电动机定子、转子铁心损耗和永磁体涡流损耗具体数值大小，见表2。其中，电动机绕组铜耗可以通过传统的测电阻并用公式计算的方法得到。转子的铁耗较小，仅为定子铁耗的0.89%，可以忽略不计；铜耗的数值最大，占整体电磁损耗的一半。

表2 额定工况下电动机内各部件的电磁损耗分布（%）

轮毂电动机温度场分析

1.复杂部件的简化与等效

（1）定子槽绕组模型的简化与等效。在建立温度场分析模型时，定子槽中的绕组和绝缘体结构复杂，很难对其进行精确建模和导热系数的计算，可以将绕组等效为一整快导体，绝缘体按体积等效成等体积的包围层，并平行紧贴于槽壁，简化模型如图4所示。

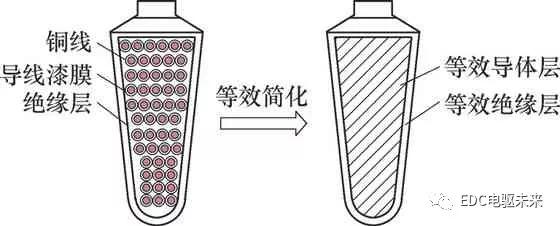
图4 定子槽绕组模型等效简化

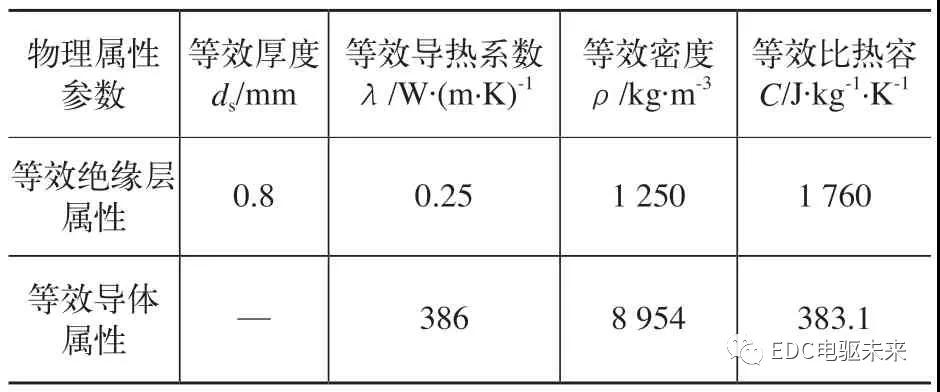
根据传热学定理，通过相关公式得到等效后的绝缘层和导体的物性参数，计算得到等效绝缘体的等效结构尺寸和等效物性参数，见表3。

表3 定子槽绕组等效模型的等效物性参数

（2）铁心叠片模型的等效与简化处理。定子铁心是由多层硅钢片经过叠压而成的，结构比较复杂。根据传热学定理，可以将铁心叠片等效成具有轴向、周向和切向不同导热性能的结合体。

可以通过公式计算得到定子铁心在各个方向上的导热系数。

通过计算得到等效模型物理属性参数见表4。

（3）轮毂电动机其他部件的等效与简化。为了使温度场分析时的有限元模型较易求解，所以对轮毂电动机中温度场分析影响较小的次要部分进行一定的省略和简化，主要体现在几个方面：忽略对整体模型影响较小的小尺寸零件，如螺栓、垫片等；忽略电动机外壳的两边端盖，以等效散热系数等效两边端盖的散热作用，保留与电动机转子相接触的顶部外壳；假设电动机内部有装配关系的零件是相互接触紧密、无空隙的。

对轮毂电动机实际结构进行简化与等效处理后得到的简化模型，如图5所示。

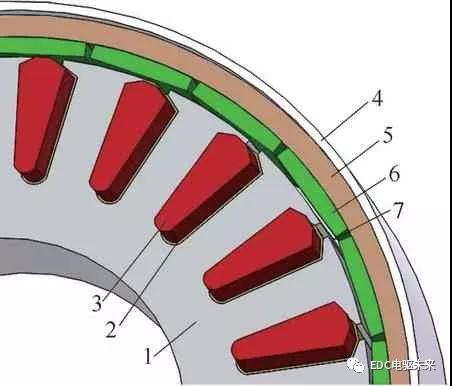
图5 轮毂电动机简化模型

1.定子 2.绝缘体层 3.导体块 4.外壳 5.转子 6.永磁体 7.气隙

2.对流换热系数的等效与计算

轮毂电动机主要的对流换热边界面为机壳外表面、机壳端面、转子端面、转子内表面、永磁体端面、气隙端面、绕组端部内表面、绕组端部外表面和定子端面。

（1）气隙散热系数的计算。随着电动机转子的旋转，电动机气隙中的空气会流动，由于气隙的尺寸较小，很难在温度场计算时模拟气隙的旋转和运动，因此对定转子间的气隙做静止处理。

（2）轮毂电动机外壳表面散热系数的计算。电动机壳在旋转时通过对流的形式与外界环境发生热交换，同时旋转电动机的外壳会加速周围空气的流动从而增强散热效果。

通过公式计算得到电动机对流散热边界面的散热系数，具体数值见表5。

表4 定子铁心简化模型物理属性参数

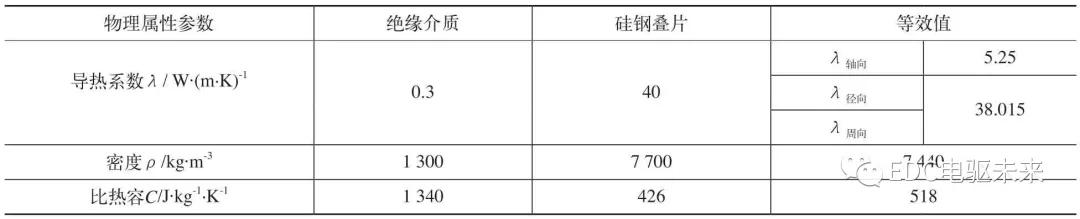
表5 轮毂电动机各边界面对流散热系数 （单位：W/m2·K）

额定工况下轮毂电动机温度场仿真结果分析

进行瞬态温度场求解后，得到额定工况下的轮毂电动机运行3 600s时的最高温升变化曲线，如图6所示。电动机的最高温升随时间成递增趋势，在前半段电动机的温升速率较快，在后半段逐渐趋于稳定，在3 600s时的最高温度为122.23℃，最高温升为99.747℃。样机的绝缘材料耐温等级为B级，即最高允许温度为130℃，所以电动机在额定工况下连续工作1h时间是安全可靠的。

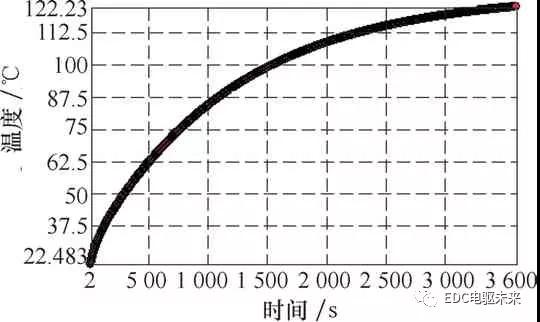
图6 额定工况下的电动机温升变化曲线

整体温度分布云图和各部件的温度分布云图，如图7所示。从温度场仿真结果可知，绕组部分的温度最高，这和损耗分析时绕组是电动机中最大热源的结果一致：绕组最高温度为122.23℃，最低温度为121.45℃。由于槽绝缘的隔热作用，绕组的最高温度区域出现在绕组中间位置，最低温度区域出现在两端，但是绕组的温度差异较小，整体温度分布较为均匀。

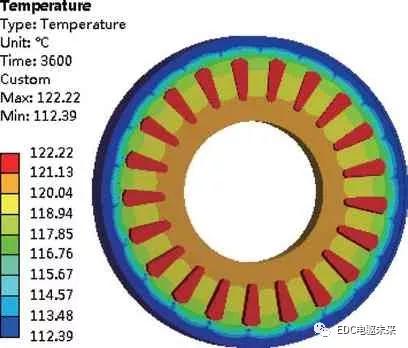
图7 电动机整体温度分布

定子的最高温度区域出现在槽底部与定子轭内圆之间的位置，因为定子的位置与绕组位置最接近，并且定子本身也是发热源，所以定子的最高温度仅次于绕组，最高温度为120.78℃。

永磁体的温差较大，最高温度为118.22℃，最低温度为113.24℃。由于磁极内圆处接近温度较高的定子，外圆接近散热较好的转子与外壳，所以磁极内圆与外圆形成了一个4.98℃的温差范围。

试验验证

为了验证本文轮毂电动机温度场仿真方法的正确性，需要对轮毂电动机进行温升试验。运用温度传感器埋入绕组端部，以检测端部温度变化，并运用红外温度计测量电动机外壳温度。试验所用的检测平台为轮毂电动机综合性能试验台，该试验台由测功仪、控制器、试验架、温度传感器等部件组成。

为了减小试验值和仿真值的对比误差，则需要使试验条件和仿真条件基本相同，控制实验室初始环境温度为22℃。在试验过程中运用测功仪和控制器配合，使轮毂电动机在额定负载工况下连续平稳运行1h，并以5min为时间段记录温度数据。将得到的温升试验结果与仿真结果进行对比，对比曲线如图8所示。

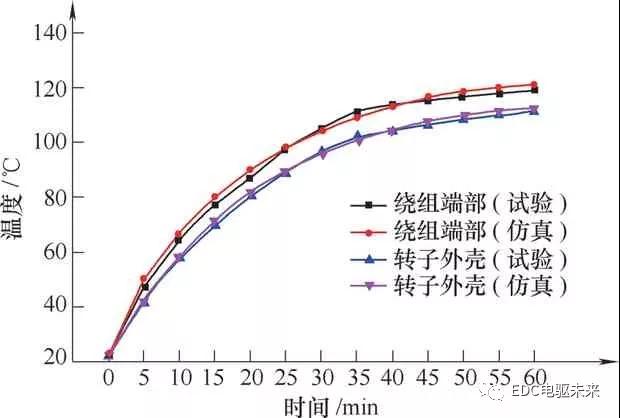
图8 轮毂电动机温度试验与仿真对比曲线

由图8轮毂电动机温升试验与仿真的对比曲线可知，转子外壳的仿真结果与试验结果几乎一致，误差在2%以内。绕组端部的仿真误差较大，最终稳定时的误差相差约2.2，但整体误差在5%以下，该结果在工程计算的误差允许范围内。所以与通过试验结果的比对，验证了本文采用的磁-热耦合仿真计算轮毂电动机温度场的方法的正确性，同时也验证了该方法能够运用于电动机初期设计中，并且能为轮毂电动机散热结构的设计提供重要的参考依据。

结语

本文通过磁热耦合的方法，对一台4kW电动汽车用轮毂电动机的温度场进行了研究，得出以下结论：

1）通过将轮毂电动机温度场的仿真结果和试验结果进行对比，验证了本文用电磁损耗为热源和散热系数相结合的磁热耦合分析方法的正确性。

2）仿真误差低于5%，验证了本文运用简化模型和散热边界条件计算方法的正确性。该方法能够有效增加求解速度，并保证求解精度。

3）本文采用的磁热耦合分析的方法，能够快速准确得到轮毂电动机各部件的温度场分布情况，能够为轮毂电动机冷却结构的设计提供重要的参考依据。