在新车型进行造型分缝设计时，由于实际零部件工艺性的原因，所有的零部件都必须设计R角，在某些接口区域，由于圆角半径比较大，零部件比分缝位置回退，就自然形成了一块无零部件覆盖的区域，称为可视三角洞现象。由于三角洞会造成感知评价下降，进而影响对产品的正面评价。本文以此为研究方向对影响三角洞面积的因素进行分析，为优化改善感知质量提供参考意见。

建立研究对象

车身前部翼子板与前照灯、前保险杠共同配合处，以及车身后部侧围外板、后保险杠及后尾灯共同配合处的分缝线均由灯的边界线生成，并和侧围或保险杠上的特征线相协调。

在图中的缝隙聚集区域，即三个或以上分缝线交汇在一起时，受塑料件、冲压件及外饰件的R角工艺限制及彼此配合间隙等影响，很容易出现三角洞(即平时所说的“老鼠洞”)现象。本文以后尾灯与侧围和后保险杠的尖角配合处形成的三角洞为研究对象对其分析，图1为实车装配后的三角洞效果。

对车身侧围、后尾灯及后保险杠形成的三角洞区域进行数学分析，将实物转化为可以进行分析的平面模型，并在模型中绘制三角形以最大限度覆盖孔洞，为了便于计算孔洞面积，此处将三角形设置为直角三角形，如图2所示。

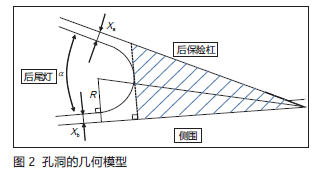
假设Xa为尾灯与后杠的距离，Xb为尾灯与侧围的距离，R为尾灯的圆角半径，α为尾灯的圆角度，阴影区域为需要计算的三角区域的面积S△。

通过几何推导计算三角形面积，该区域S△数学表达式如下所示：

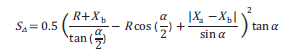
变量分析

根据上述的孔洞面积公式可知，孔洞的大小与尾灯的圆角半径R、尾灯与侧围的距离Xb、尾灯的圆角度α以及尾灯与后杠的距离Xa等变量有关，针对这四种变量，现分别分析其对孔洞面积的影响。

1.尾灯圆角半径R的影响

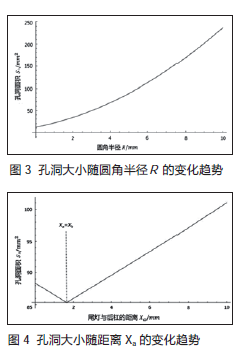
当尾灯与后杠的距离Xa、尾灯与侧围的距离Xb、尾灯的圆角度α为固定值，圆角半径R的影响变化曲线如图3所示。

如图3所示，三角洞面积随着圆角半径R的变化呈半抛物线形变化,随着圆角半径的不断增大，三角洞的面积也随之增大，同时灯具的重量会随之减小，一般对灯具的尖角部位加工工艺要求最小是0.5 mm。

2.尾灯与后杠的距离Xa的影响

当尾灯与侧围的距离Xb、尾灯的圆角度α、尾灯的圆角半径R为固定值时,尾灯与后杠的距离Xa的影响变化曲线如图4所示。

如图4所示，当Xa＜Xb时，随着Xa距离的增大，孔洞面积逐渐减小，当Xa-Xb=0时，孔洞面积达到最小值。当Xa＞Xb时，随着Xa距离的增大，孔洞的面积会越来越大，感知质量也会随之越来越低。

3.尾灯与侧围的距离Xb的影响

当尾灯与后杠的距离Xa、尾灯的圆角度a、尾灯的圆角半径R为固定值时，尾灯与侧围的距离Xb的影响变化曲线如图5所示。

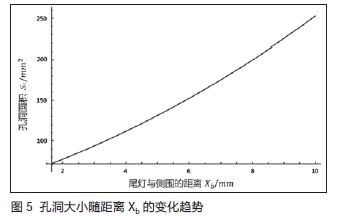
如图5所示，三角洞面积随着尾灯与侧围间隙的变化近似呈直线形增长。随着间隙的不断增大，三角洞面积会随之增大，给用户的视觉感知质量就会越来越差。

4.尾灯的圆角α的影响

当尾灯与后杠的距离Xa、尾灯与侧围的距离Xb、尾灯的圆角半径R为固定值时，根据α的影响变化曲线可知，尾灯尖角部分角度多为锐角，当角度越小的时候三角洞面积会越大。一般要求侧围外板后尾灯尖角角度不能小于35°。

三角洞的优化

分缝线的汇合聚集必然会导致出现三角孔洞的现象，这是不可避免的，但这不一定是缺陷，只有引起客户不悦的情况才能定义为缺陷。多数情况下，经过一系列的优化设计可以降低客户的视觉敏感度，降低三角洞缺陷，成为可接受的造型方案。

对三角洞的优化，一方面可以根据三角洞面积公式，对各个变量参数进行合理设置。

1)根据图3可知，优化尾灯圆角的半径R达到最小，可以减小孔洞的面积，根据目前的工艺能力，圆角半径最小要求为0.5 mm，这对灯具供应商的制造成本并无影响。

2)结合图4、图5可知，优化尾灯与后杠及尾灯与侧围的距离，当两者距离相等时，不仅使得孔洞的面积是最小的，而且间隙过渡的均匀性会提升用户的感知评价，如果两侧的间隙不等，很容易在尾灯尖角过渡的地方形成喇叭口，给用户造成很差的视觉印象。 

3)对尾灯圆角度α的优化。在不影响车型开发整体效果图的情况下,建议α≥35°，可以有效避免三角洞现象。

另外一方面可以在造型阶段通过修改分缝线来避免三角洞或者增加黑色胶条，或者对尾灯边缘进行“熏黑”处理的方法均能达到减弱三角洞的敏感度，对此本文不再详细阐述。

结束语

为提升感知质量，使得零件之间的配合更加精致细化，本文通过建立数学公式的方式从理论上为改善车身外表面三角洞现象提供了一种思路，为工艺、产品等专业部门对车身外观评审提供参考。