燃料电池空压机悬置子系统分析及优化
文章来源:汽车燃料电池之家
发布时间:2020-11-30
对燃料电池空压机悬置子系统采用ADAMS 进行建模,计算其刚体模态和解耦率。模态间隔不满足要求的情况下,使用ADMAS/Insight 进行多目标优化。
对燃料电池空压机悬置子系统采用ADAMS 进行建模,计算其刚体模态和解耦率。模态间隔不满足要求的情况下,使用ADMAS/Insight 进行多目标优化。悬置刚度优化后解耦率所有方向大于80%,转子转动方向达到94%,模态频率分布避开路面和空压机本体怠速激励,前6 阶模态间隔大于1Hz。对该悬置系统进行7 种极限工况运算,求出其位移和受力分布,为燃料电池系统布置提供理论依据。
0 引言
由于汽车排放问题的日益突出,世界各地十分关心新能源技术,燃料电池汽车属于零排放车型,他与内燃机车有着相近的续航里程[1],从而备受关注,成为未来汽车的发展方向。燃料电池的工作原理为将氢气和氧气通过电极反映直接转化为电能并产生水[2]。由于没有发动机工作时不平衡力和力矩的主要激励源,燃料电池车通常被认为具有低噪声的优势。但是,与传统内燃机车相比,燃料电池汽车总体声压级并无明显优势,且声品质较差[3]。其中,空气压缩机为燃料电池车的主要噪声源。
空压机悬置作为连接空压机和燃料电池总成之间的弹性系统,主要用于支撑和隔振,其隔振性能的优劣将直接影响燃料电池总成的耐久和NVH 性能,因此空压机悬置设计是燃料电池汽车减震降噪中不可忽视的环节。目前开展的悬置研究工作大部分针对传统汽车[4],本文以某燃料电池空压机系统悬置作为研究对象,建立了燃料电池悬置系统的仿真模型,采用ADAMS 进行分析,对悬置系统的固有频率和模态解耦率进行动力学求解及优化。
1 空压机悬置子系统动力学模型
某燃料电池空压机系统物理模型如图1 所示,采用4点支撑方式,序号1,2,3,4 对应4 个悬置,悬置的弹性中心方向与主坐标方向相同。XYZ 是定义的空压机总成坐标系,O 为总成的质心位置,X 轴指车辆前进方向,Y 轴指车辆宽度方向,Z 轴为垂直方向。
图1 燃料电池空压机悬置子系统动力学简化模型
空压机总成有6 个自由度,分别是X,Y,Z 方向平动x,y,z,以及X,Y,Z 方向的转动α,β,γ。故悬置广义坐标可表示为:
假设空压机是作为刚体,忽略其阻尼影响,则自由振动方程可简化为[5]:
当悬置系统在第i 阶固有频率振动时,第k 个广义坐标振动能量占系统总能量的百分比为[6]:
Tki 的大小反映了某k 个自由度上振动能量耦合程度,也就是反映了振动形式下的耦合情况[7]。如果Tki=100%,则表示第i 阶模态在k 个自由度上完全解耦。
2 空压机总成仿真分析
2.1 空压机悬置系统设计目标
传统燃油车动力总成模态分布在6-30Hz[8],燃料电池不同于内燃机,空压机的振动情况不同于传统燃油车动力总成,总体设计思路应该是:避开空压机工作转速范围,避免共振;在激励较大的方向,悬置总体刚度较小,降低传递给电堆的振动;在激励较小的方向,悬置总体刚度较大,保证空压机的支撑。根据隔振理论,悬置设计目标如下:
②前六阶能量解耦率要达到80%,空压机转动方向要达到90%;
2.2 空压机总成基本参数
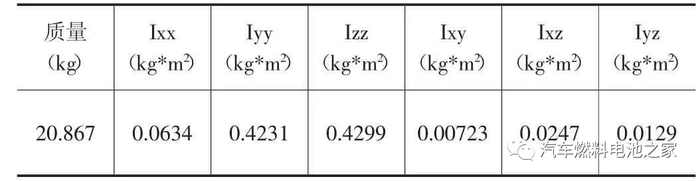
该系统由电机总成和压缩机总成组成,在ADAMS 建立模型时,将系统视为具有六个自由度的刚体,系统相关参数如表1 所示。
悬置的4 个橡胶软垫由bushing 单元代替,静刚度为100N/mm,动静比1.4,bushing 单元初始XYZ 三个方向刚度为140N/mm。
2.3 空压机总成模态分析
模态分析在ADAMS/Vibration 中进行,依次选择plugins -> test -> vibration analysis,利用normal mode analysis 进行模态和解耦率分析,得到其前六阶固有频率以及每个方向的解耦率,仿真结果如下表2 所示:
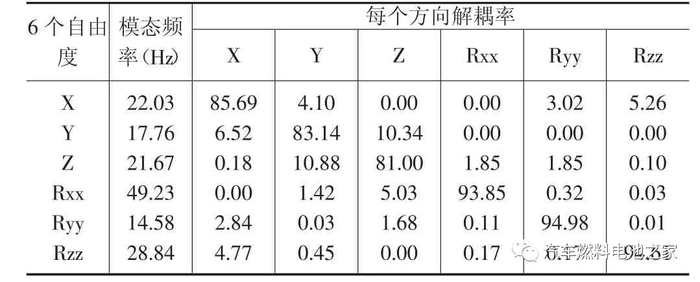
此方案各个方向的解耦率比较好,均大于80%。且空压机转动方向Rxx 解耦率大于90%,但是X 和Z 方向模态间隔只有0.36Hz,不满足设计要求,需要进行优化设计。
3 优化设计
3.1 目标函数
本文以前6 阶解耦率作为优化设计目标函数,表示如下:
3.2 设计变量
由于燃料电池的空间布置原因,本文的安装位置和角度不做调整,主要改变悬置各个方向的刚度。考虑悬置安装特性,前悬置2 个减震垫相同,后悬置2 个减震垫相同。减震垫轴向对称,周向X 和Y 向刚度相同,Z 方向为轴向刚度。因此前悬置2 个刚度变量Kr1、Kz1,后悬置2 个刚度Kr2、Kz2,使用ADAMS/Insight 对4 个刚度进行解耦优化。
3.3 约束条件
①刚度约束:考虑到橡胶悬置的材料和工艺,以及空压机高频振动特性,悬置的刚度在20~200N/mm 之间。
②位移约束:为了防止空压机运行时与其他部件发生碰撞,防止振动过大,系统各个方向位移必须小于5mm。
③频率约束:空压机的怠速转速为3000rpm,路面在高速时激励为5~10Hz,综合前文中的设计目标,系统频率应该在10~50Hz 之间,模态间隔在1Hz。
3.4 优化结果分析
经过优化仿真DOE,优化后的悬置刚度如表3 所示,总体上悬置的刚度减小,个别方向变大。
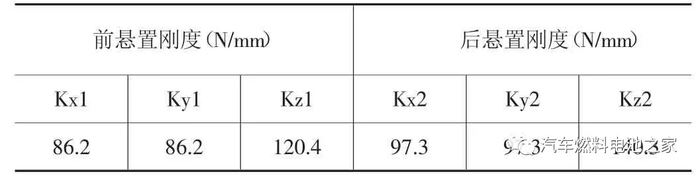
优化后的固有频率和解耦率分布见表4。通过表4 和表2 的对比,可发现某些方向固有频率降低,一阶模态大于10Hz,可以避开路面激励,6 阶模态为45.82Hz,小于空压机怠速激励50Hz,且模态间隔均大于1Hz,满足模态要求。系统解耦率在各个方向均大于80%,空压机转动方向Rxx 大于90%,满足解耦率要求。
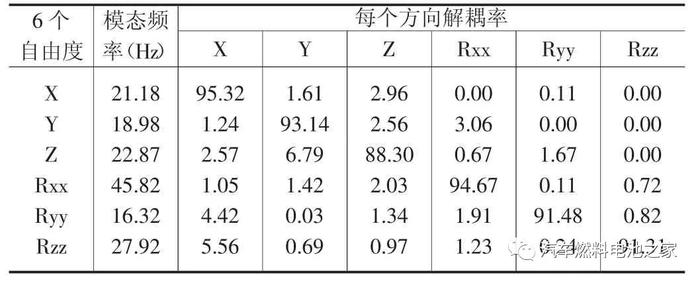
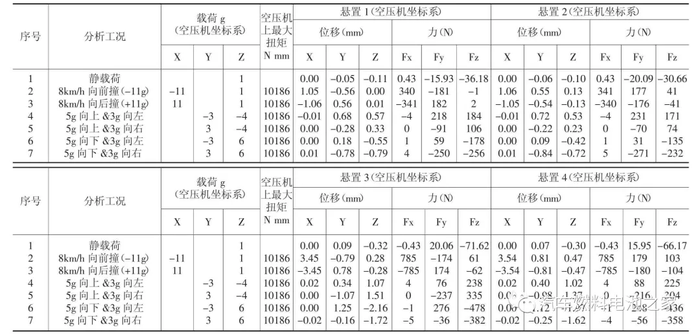
本文借鉴某公司规定的28 工况,选取6 极限工况和静载下工况,计算4 个悬置点的位移和受力情况,优化后极限工况和静载结果如表5 所示。
在静态只受重力情况下,悬置3 和4 靠近质心,承受主要载荷。6 种极限状态下,4 个悬置XYZ 方向上的最大位移分别为3.54mm、1.26mm、2.16mm,所有位移均小于5mm,满足设计要求,空压机本体不会与其他零件发生碰撞。
4 结束语
综上所述,应用ADAMS 对燃料电池空压机悬置子系统进行刚体模态和解耦率进行求解,使用ADAMS/Insight隔振优化设计,使得模态间隔达到目标值,模态分布更加合理。通过悬置极限工况计算,可以得到每个悬置点的受力和位移变化。利用这些结果,可以校核支架和橡胶的强度。求出空压机的最大位移,为燃料电池系统布置提供理论依据和设计参考。















正在获取数据......