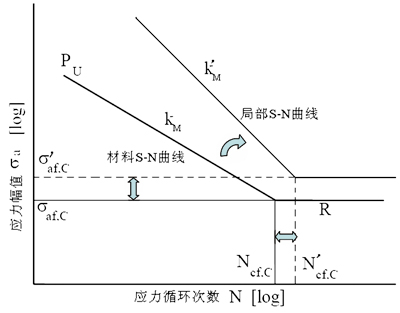
图1 材料S-N曲线的修正

随着数值计算方法的日益成熟和计算机技术的迅速发展，数值仿真技术被越来越广泛地应用到工程技术的各个领域。在发动机开发过程中合理地采用数值仿真手段可以有效地缩短开发周期、降低开发成本和减小设计风险。

发动机作为一个复杂的系统，其正常运转依赖于各个子系统的相互协调，发动机附件通常被安装在发动机本体上，为了优化发动机的各项性能，通常需要在设计阶段就对附件的安装位置进行调整优化。因此，如何保证本体给附件提供足够的支撑强度以保证发动机正常运转是发动机设计过程中的一项重要内容。

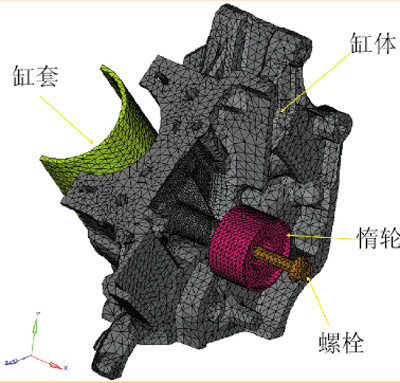
图2 有限元分析模型

本文采用有限单元法和基于有限元的疲劳分析方法对某款V6发动机正时轮系的惰轮凸台进行了数值仿真计算，计算结果与实验结果完全一致。

疲劳分析理论

现有的疲劳分析软件大多数是基于有限元分析的，疲劳计算通常是在有限元单元节点上进行，节点的应力张量是疲劳计算的输入。由于裂纹通常从构件表面产生并扩展，同时，为考虑局部的应力梯度影响，疲劳计算往往仅在构件表面及其表面下面一层的节点上进行，为此，在实施疲劳计算之前需将材料S-N曲线转换成局部节点处的S-N曲线，如图1所示。

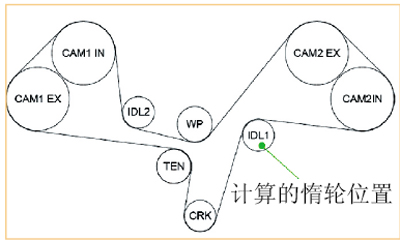
图3 正时轮系布置示意图

节点处的局部S-N曲线是通过考虑各种影响因素对材料S-N曲线进行修正得到的。各种因素对材料S-N曲线的修正均可以归结为对S-N曲线的三个决定性参数的影响函数，即材料的耐久应力极限σaf,c、耐久循环极限Ncf,c以及S-N曲线的斜率KM的影响函数。由于疲劳分析的复杂性，这些影响函数多数是基于大量试验的经验公式。

1、耐久应力极限修正

其中，σaf,c为节点S-N曲线的耐久应力极限，σA,tsc为材料的交变应力极限，ƒgs,af为普通表面因素，ƒgr,af为应力梯度因素，ƒm,af为平均应力因素，ƒst,af为统计特性因素，ƒti,af为热效应因素，ƒtp,af为技术处理因素，ƒ1,af为表面粗糙度和锻造度综合影响因素，ƒ2,af为表面热处理工艺综合影响因素。

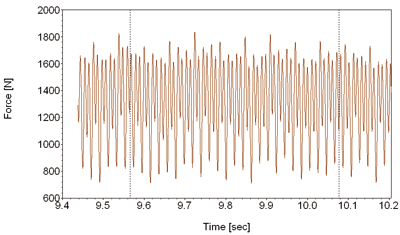
图4 惰轮受力时间历程

2、S-N曲线斜率修正

其中，kM为材料S-N曲线的斜率，kc为节点S-N曲线的斜率，IFK2、IFK3为材料参数，ƒm,sf为平均应力影响因素， ƒgs,sf为应力梯度影响因素。

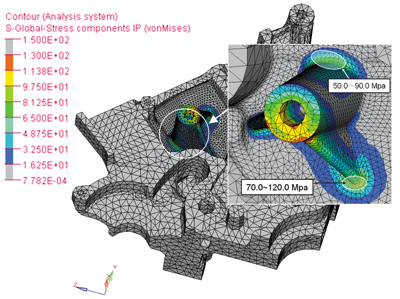
图5 峰值作用力下结构应力分布

3、耐久循环极限修正

对铸铁材料耐久循环极限的修正如下：

其中，Ncf,c为节点S-N曲线的耐久循环极限，Ncf,M为材料S-N曲线的耐久循环极限，Fakt21为热机影响因素， ƒm,sf为平均应力影响因素，ƒm,cf为平均应力对耐久循环极限的影响因素。

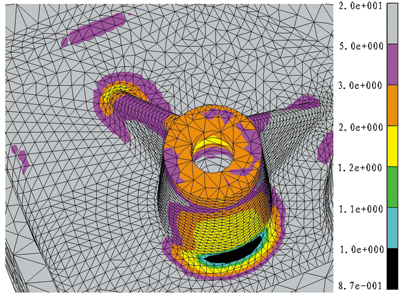
图6 疲劳安全因子分布

#p#分析模型

为获得疲劳分析的输入数据（节点处的应力状态），需要对结构进行有限元求解计算。结构有限元分析的模型如图2所示，主要包括缸体、缸套、惰轮和螺栓。为了在保证计算精度的同时尽量减少模型规模，文中将V6发动机的结构切出一部分，并在非关键区域采用了较疏的网格。

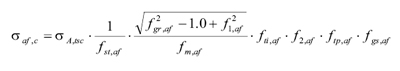
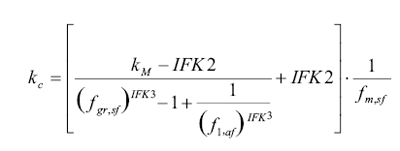
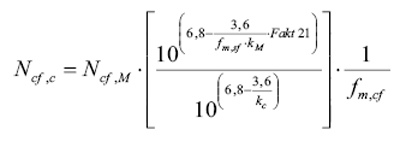
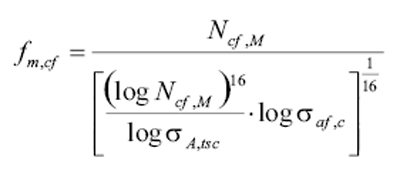
#p#部件之间的相互作用主要采用ABAQUS软件提供的有限滑移弹性接触模型以及耦合方程来实现。相关切面采用对称边界条件来限制结构的缸体位移。结构承受的载荷主要是静态的螺栓预紧力和皮带轮张紧后振动造成的动态作用力。计算考虑的惰轮位置如图3所示。惰轮的受力是通过一维动力学计算获得的，该作用力的时间历程如图4所示。

使用上述有限元模型组织成两种计算工况对结构实施线弹性静力学求解。第一种工况为峰值作用力工况，惰轮受力1800N；第二种为谷值作用力工况，惰轮受力650N。

图7  试验台架上凸台断裂实物

疲劳分析采用同样的网格模型和两种工况下的应力结果作为输入，综合考虑平均应力、表面粗糙度和S-N曲线的统计特性对局部S-N曲线的修正。其中，螺栓预紧力作为静态应力，并通过两种动载工况的线性组合获得平均应力和应力幅值。

结果分析

结构在峰值作用力工况下的应力分布如图5所示。计算结果表明，该结构在峰值作用力下的应力值较小，最大应力值为150Mpa，在材料的许用应力（250Mpa）范围之内，满足静强度要求。

结构的疲劳安全因子分布如图6所示。从图中可以看出，黑色区域的疲劳安全因子较小，最小值为0.87，达不到设计要求，且此处的应力历程表明，该部位的应力一直以拉应力占主导，容易滋生裂纹并扩展。因此，需要对结构进行修改。

该方案下的凸台在台架试验时发生断裂，如图7所示。从断裂面的层次来看，凸台在发动机运行过程中产生了疲劳破坏。裂纹扩展区产生的时间较早，并由于流入机油而呈现深色，脆段区颜色较浅。可见，分析模型较为准确地捕捉到了该方案的设计缺陷。建议在凸台现有加强筋的对称方向增加两个加强筋以改善结构的应力分布。

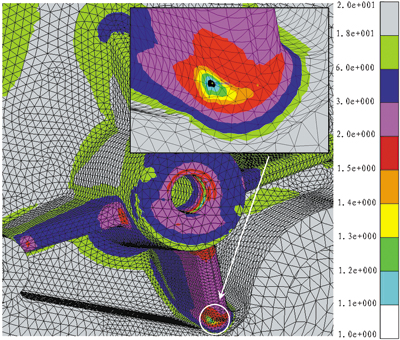
图8  修改方案的疲劳安全因子分布

修改方案及其计算结果

根据原方案分析结果和建议对结构的网格模型进行局部修改后，按照相同的边界条件和计算工况实施有限元计算和疲劳分析，得到修改方案的疲劳安全因子分布如图8所示。

从图8中可以看出，添加加强筋后，结构的承载特性得到了改善，结构的疲劳安全因子集中在纵向加强筋的底部倒角区域，最小值为1.098，满足要求。该区域的抗疲劳特性会由于铸造时的光滑过渡而得到进一步改善。

结论

合理地组织有限元分析工况，使用有限元分析结果对发动机附件进行疲劳分析获得了较高的计算精度。文中通过直接修改网格模型的方法对模型的局部改进提高了计算分析的效率。发动机台架试验的结果证实了计算方法的可靠性和精确性。采用数值仿真手段准确预测发动机开发过程中的设计缺陷，缩短了开发周期、降低了设计风险。