曲轴是发动机的关键零部件之一，曲轴的强度直接决定了发动机的工作性能和使用寿命。同时，曲轴也是受工作载荷最为恶劣的零部件之一，在周期性变化的气体力、惯性力和力矩作用下，曲轴内部会产生交变的弯曲应力和扭转应力，应力过大将会导致曲轴失效，继而引起整机的损伤破坏。

在曲轴所承受的各种载荷中，轴颈处的油膜压力和曲轴旋转惯性力是最主要的载荷，油膜压力是计算曲轴应力的关键。本文基于多体动力学理论，综合考虑轴承弹性流体润滑，建立某单缸光学发动机曲轴系的动力学分析模型，计算曲轴在各个转角下的位移应力值，并将该结果作为曲轴疲劳强度计算的输入载荷，在考虑材料强化处理、应力循环和尺寸的影响下，根据材料的疲劳极限，计算出曲轴危险部位的最小安全系数。

这种计算方法更符合曲轴实际受力状况，同时，在强度计算时利用圆角子模型代替整个曲轴，计算模型的网格数大幅度减少，有效提高了分析效率。

曲轴系多体动力学分析

1.液体润滑计算理论

在求解曲轴轴颈处的油膜压力分布时，控制方程采用扩展雷诺方程：

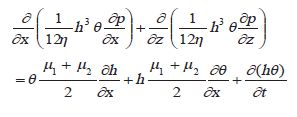
P：油膜压力;

η：机油动力粘度;

h：名义油膜厚度;

θ：机油填充率;

μ1，μ2：轴颈、轴瓦的周向运动速度。

扩展雷诺方程表征了油膜厚度与压力、表面速度、间隙变化率之间的关系，载荷越大，油膜压力越高，油膜厚度越小。

2.曲轴动力学模型

在AVL-EXCITE&PU中建立曲轴多体动力学计算模型，包括曲轴、连杆、活塞、飞轮和缸体。其中，

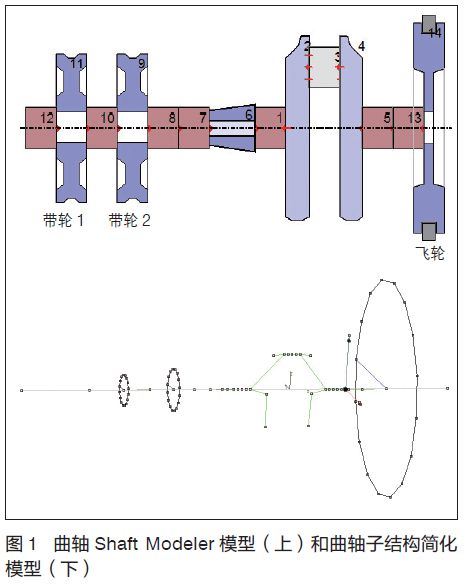
曲轴模型采用EXCITE软件自带的Auto shaft和Shaft Modeler模块建立：首先通过Auto shaft将曲轴识别分割成主轴颈、曲柄销、曲柄臂;然后通过内置有限元求解和刚度计算，在Shaft Modeler中输入材料属性及几何信息，得到曲轴的简化模型;飞轮因其结构的规则性，在Shaft Modeler中以参数的形式输入，包括：质量、惯量和相对位置(见图1)。

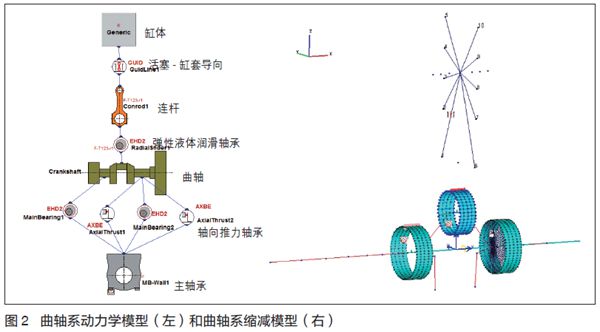
主轴承和连杆均采用有限元缩减模型，缸套用固定位置的刚性点代替。该单缸机曲轴包括两个主轴颈段和一个曲柄销段，主轴颈与主轴承座、曲柄销与连杆大头瓦之间均采用弹性液体润滑轴承EHD2连接，第二主轴颈附加AXBE止推轴承传递轴向力(见图2)。

3.曲轴动力学计算结果

在设计阶段，重点关注曲轴在发动机最大转速下的疲劳强度，因此本文计算工况为发动机最大转速3 000 r/min。本计算模型为四冲程单缸发动机，动力学仿真分析两个工作循环，为避免第一个循环周期的不稳定，计算结果只提取第二个工作循环。

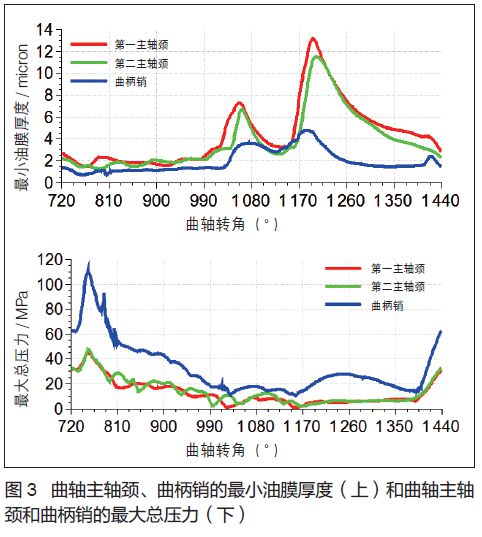
最小油膜厚度是评价轴承润滑状况的一个重要指标，油膜厚度太低会造成润滑不良。曲轴主轴颈和曲柄销的最小油膜厚度和最大总压力，曲柄销处的油膜压力较大，油膜厚度较薄。由此可知，油膜压力越大，油膜厚度越小(见图3)。曲轴动力学结果将为曲轴疲劳强度计算提供载荷边界。

曲轴疲劳强度计算

零部件的疲劳强度取决于应力大小和应力幅值、零件的几何形状、零件表面加工精度以及材料性能等因素。在发动机运转中，曲轴承受交变载荷的作用，其疲劳破坏基本都发生在曲柄臂的圆角和油孔边缘等几何突变处，其中以圆角处最为明显。为了提高计算精度和效率，本文采用圆角子模型的方法对曲柄臂的圆角处进行精细网格化和疲劳分析。

1.圆角子模型

该单缸发动机有两个主轴颈圆角和两个曲柄销圆角，分别建立各曲拐的主模型和圆角子模型网格(见图4)。

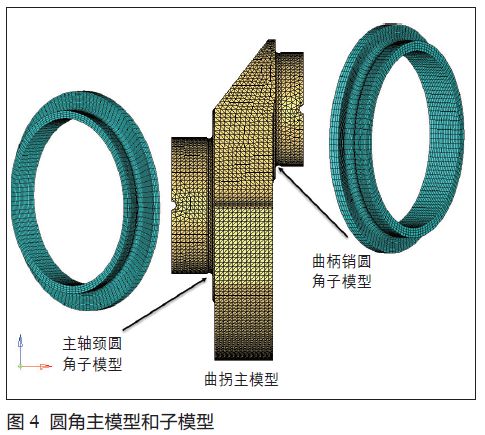
2.应力场计算

应力计算采用Abaqus软件，加载时，首先约束半曲拐主轴颈中心，在曲柄销中心施加X、Y、Z三个方向的单位位移和载荷;再约束曲柄销中心，在主轴颈中心施加X、Y、Z三个方向的单位位移和载荷。由此得到半曲拐在12个单位位移和载荷下的应力场，然后使用曲拐主模型的位移边界驱动圆角子模型应力计算，得到圆角子模型在12个单位位移载荷下的应力分布。

3.安全系数计算公式

曲轴的安全系数即曲轴强度的储备系数，它表示曲轴本身的疲劳强度与工作应力的比值。圆角安全系数计算公式如下：

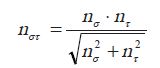
只考虑弯曲时的安全系数：

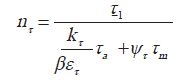
只考虑扭转时的安全系数：

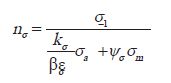
nστ：弯曲扭转组合交变应力下轴的工作安全系数;

nσ：对称弯曲下轴的工作安全系数;

nτ：不对称扭转下轴的工作安全系数;

σ-1，τ-1：曲轴材料对称循环弯曲和扭转疲劳极限;

kσ，kτ：分别为弯曲和扭转时圆角处的应力集中系数;

β：强化系数，表明不同加工方法和工艺措施对曲轴圆角部位疲劳强度的影响;

εσ，ετ：绝对尺寸影响系数，表明因实际曲轴的绝对尺寸与试件不同时，两者的疲劳极限百分比;

σa，τa：正应力、剪应力幅;

σm，τm：平均正应力和平均剪应力;

ψσ，ψτ：材料对应力循环不对称的敏感系数。

4. 疲劳计算

通过有限元计算得到圆角子模型的单位位移静态应力，从动力学计算结果中提取出动态位移的历史载荷谱，将应力计算结果和动态位移载荷谱输入疲劳计算软件FEMFAT的Channal Max模块中进行应力合成和疲劳分析。影响因素设置有：表面粗糙度2 μm、工艺尺寸7.5 mm、离散度1.35、圆角滚压系数1.8，存活率为99.99%。

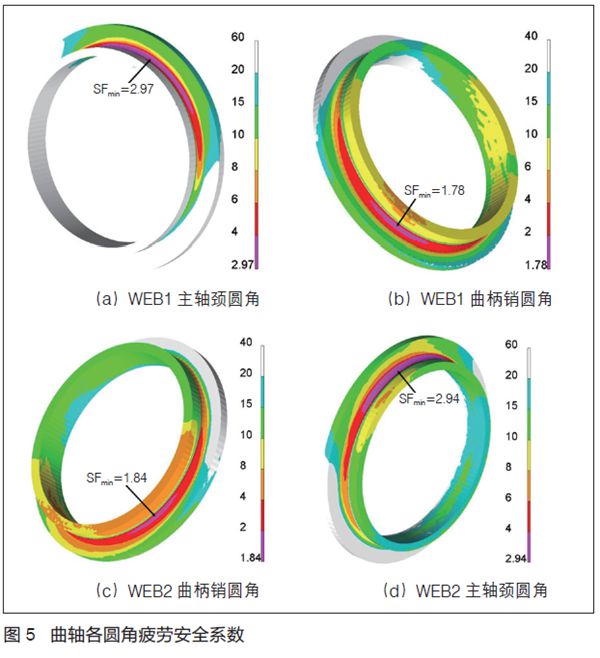
本单缸机只有一个曲拐，从机体前端往后端依次命名各半曲拐为WEB1和WEB2，疲劳计算结果如图5所示。考虑到载荷的离散度以及模型精度，曲轴圆角最小疲劳安全系数SFmin需大于限值1.1。计算结果显示：曲轴上各个圆角最小疲劳安全系数分别为2.97、1.78、1.84、2.94，均满足1.1的限值要求;曲柄销圆角最小安全系数均小于主轴颈圆角，除了几何形状的区别外，由动力学计算结果可以发现，曲柄销所受的油膜压力大于主轴颈的油膜压力，这是曲柄销较之主轴颈疲劳强度弱的重要原因。

结论

曲轴轴颈和曲柄连接的圆角处是曲轴应力集中最为严重的部位，也是曲轴疲劳强度最薄弱处。本文运用多体动力学软件，在机体动力学基础上耦合了非线性液体润滑，将有限元计算得到的圆角子模型的单位位移静态应力和动力学计算提取出动态位移的历史载荷谱输入到疲劳软件中进行应力合成和疲劳计算。这种计算方法较为全面地考虑了影响曲轴应力的因素，曲轴应力的计算结果更加接近实际情况。

同时，利用仿真软件也可以在模型的开发设计阶段对曲轴的疲劳强度进行预测并提供优化思路，节省大量时间和经济成本。