图1  防尘罩有限元模型

根据Mooney-Rivlin模型得到防尘罩的材料特性参数，利用ANSYS软件对防尘罩在一定工况下的应力分布与接触干涉情况进行模拟分析，可找出防尘罩最易拉裂的部位与最易发生磨损的部位，加速防尘罩的设计进程。

防尘罩大量应用于汽车等速万向节，与等速万向节外圈和中间轴相配，存储润滑脂并防止杂物（如泥沙等）进入万向节腔内。防尘罩在等速万向节大摆角的条件下易发生波谷拉裂、表面磨损等失效形式。由于防尘罩采用的橡胶材料本身是非线性材料，受力变形过程比较复杂，同时又涉及大位移、大应变，并且防尘罩具有几何非线性和材料非线性的双重特性，因此，传统的理论分析方法和试验方法很难及时有效地对其使用过程中的变形和应力状态进行模拟与分析。

图2  防尘罩应力与接触情况一

随着有限元技术与计算机仿真技术的结合，例如ANSYS软件，可以快速有效地进行各种线性和非线性结构的仿真分析。本文利用ANSYS软件，通过橡胶类材料的本构模型得到防尘罩材料特征参数，对防尘罩在一定工况下的应力分布与接触干涉情况进行模拟分析，找出了防尘罩最易拉裂的部位与最易发生磨损的部位。同时，对防尘罩进行了同一工况下的实验，通过对仿真结果与实验结果的比较，验证防尘罩非线性有限元分析方法的准确性。

防尘罩材料特性分析

本文所用的防尘罩材料为热塑性聚酯弹性体，热塑性聚酯弹性体又称聚酯橡胶，具有热塑性塑料的易加工性和橡胶的优良特性，如大变形、高弹性等性能。

通常用应变能密度函数W（I1，I2，I3）来表现橡胶类材料的力学特性，其中， I1、I2、I3、 为变形张量的3个不变量，其表达式分别为： I1=λ12+λ22 +λ32 ，I2=（λ1λ2）2+（λ2λ3）2+（λ1λ3）2，I3=（λ1λ2λ3）2。其中，λ1 、λ2和λ3为三个主伸长比，他们的表达式为：λi=1+εi（i=1、2、3）， εi为主轴方向应变。

图3  防尘罩应力与接触情况二

Rivilin推导出把应变能密度表示成张量不变量的级数形式：

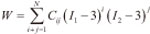
式中，Cij 为Rivilin系数。

Mooney简化了Rivilin模型，提出了Mooney-Rivilin模型，该模型是目前最常用的橡胶类材料模型：

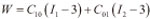
式中，C10 、 C01为Mooney-Rivilin参数，可通过试验确定。通过对防尘罩材料进行单轴向拉伸和等双轴拉伸试验，得到材料的应力应变数据，通过数据处理得到防尘罩材料的两个参数 C10=9.946，C01=-1.235。

防尘罩有限元模型

根据防尘罩结构与载荷的对称性，为了节省资源取一半防尘罩结构进行分析。一般来说，对于非接触问题常选用精度好的高阶次单元；对于接触问题，由于接触面接触条件的特殊性，在单元的选取上不能一味追求精度好的高阶单元。防尘罩形状较复杂，在摆角较大时，波谷与波谷、波峰与波峰之间会发生接触，为使模型能在节点数不是非常大的情况下，比较精确地模拟实际情况，选择SOLID185六面体单元。采用扫略网格划分的方法，在接触区域和结构关键部位将网格划分的细一些，以保证计算精度，所建立的防尘罩有限元模型如图1所示。

图4  防尘罩失效形貌一

防尘罩波谷与波谷、波峰与波峰之间的接触属于面面接触，采用面面接触的分析方法，选用TARGET170作为目标单元，CONTACT174为接触单元。通过接触向导创防尘罩波谷与波谷、波峰与波峰之间的接触对。根据对称性，在防尘罩对称面上施加对称约束，根据工况，在大端结构部位施加全约束，在防尘罩小端结构部位施加载荷，使防尘罩产生30°摆角。

防尘罩有限元分析结果

防尘罩有限元分析结果如图2、图3所示。图2中，防尘罩最大应力位于波谷1，为9.324 MPa，次应力位于波谷5，可见在波谷1最易拉裂，波谷5其次。

图5  防尘罩失效形貌二

如图3所示，防尘罩波峰与波峰之间、波谷与波谷之间有接触，受防尘罩内部润滑脂的影响，波谷与波谷之间的磨损较波峰与波峰之间的磨损要轻。波峰3在波峰2与波峰4的接触挤压下，受到最大的压应力。另外，波峰2与波峰3的接触面积比波峰3与波峰4的接触面积要小，所以，波峰3与波峰2接触的表面最易发生磨损。

防尘罩实验结果

防尘罩在摆角为30°、转速为900 r/min的条件下测试，测试550 h后防尘罩失效，失效形貌如图4～图6所示，波谷1与波谷5出现裂纹，波峰3出现磨损现象。

对比图4与图5，可以看出防尘罩波谷1处裂纹比较深，波谷5处裂纹比较浅，波谷1比波谷5拉裂严重，与图2中有限元分析结果一致。

图6  防尘罩失效形貌三

如图6所示，防尘罩波峰3与波峰2接触的表面有比较严重的磨损，与图3中的有限元分析结果一致。

从图2～图6可以看出，有限元模拟结果与实验结果吻合。由此可见，本文所采用的防尘罩材料模型、网格划分、接触和约束等方面的处理是合理的，防尘罩的非线性有限元模拟方法基本正确可信。

结语

借助有限元软件ANSYS和防尘罩的台架试验，对比分析了防尘罩在一定工况下的应力分布和接触干涉情况，取得了如下成果：

第一，通过防尘罩材料热塑性聚酯弹性体的实验和Mooney - Rivlin模型，分析得到防尘罩的材料参数C10与C01，为防尘罩的有限元分析提供了基础。

第二，建立了防尘罩的非线性有限元模型，计算了防尘罩结构在一定工况下的应力分布情况和接触干涉情况，找出了防尘罩最易发生拉裂失效和磨损失效的部位。

第三，通过防尘罩的台架试验，得到了防尘罩主要的失效方式与失效形貌。

第四，通过对有限元分析结果与实验结果的比较分析，验证了防尘罩非线性有限元分析方法的准确性，对防尘罩的设计分析具有一定的指导意义和参考价值。