知荐 | ADAS系统中自动换道控制逻辑及算法解析
文章来源:焉知汽车
发布时间:2020-03-11
为了保证自动换道能顺利实施,需要根据接收的传感器信息和智能网联控制单元(如短程通信DSRC或长期演进的V2X,LTE-V)发出的相邻车辆信息(包括位置、加速度、速度等),从而计算出相应的相应的安全行驶轨迹,同时保证在车辆安全的前提下,更加快速、平稳的变换到目标车道,对减少车辆延误、提高道路的通行效率有重要意义。

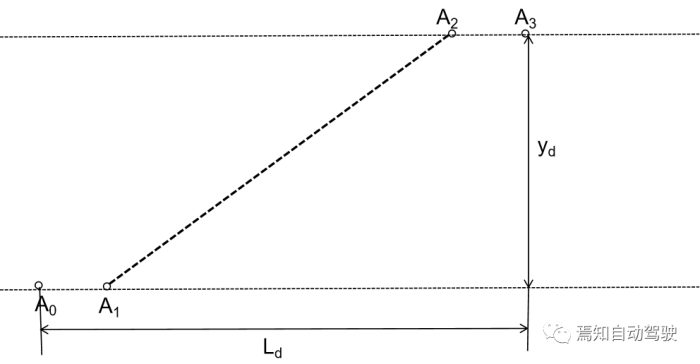
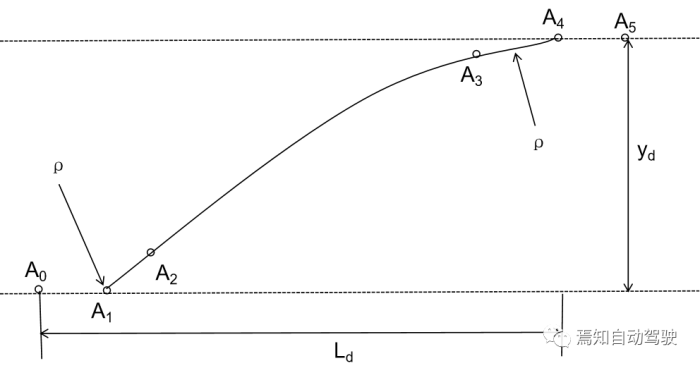
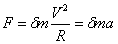
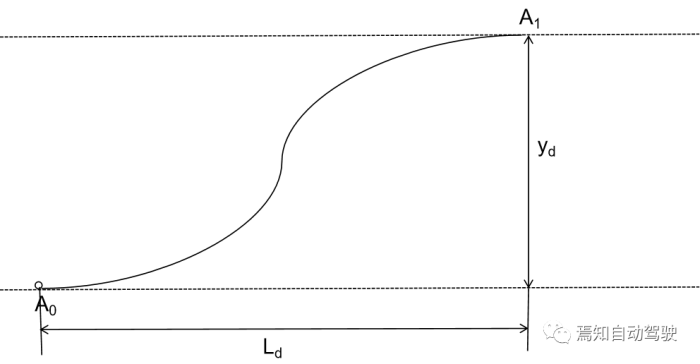
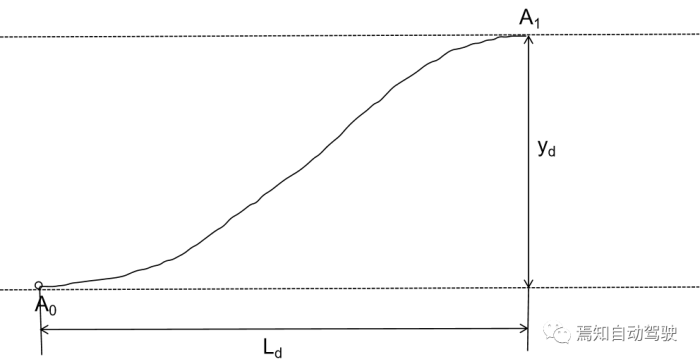
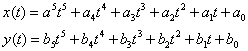
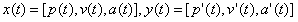 分别表示为换道起始和终止处的位置、速度和加速度集合。而实际换道过程中的边界条件为其换道轨迹起始点和终止点的位置、速度和加速度与对应的实际值或期望值相同,即
分别表示为换道起始和终止处的位置、速度和加速度集合。而实际换道过程中的边界条件为其换道轨迹起始点和终止点的位置、速度和加速度与对应的实际值或期望值相同,即
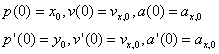
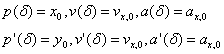
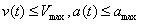
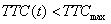
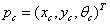 和
和
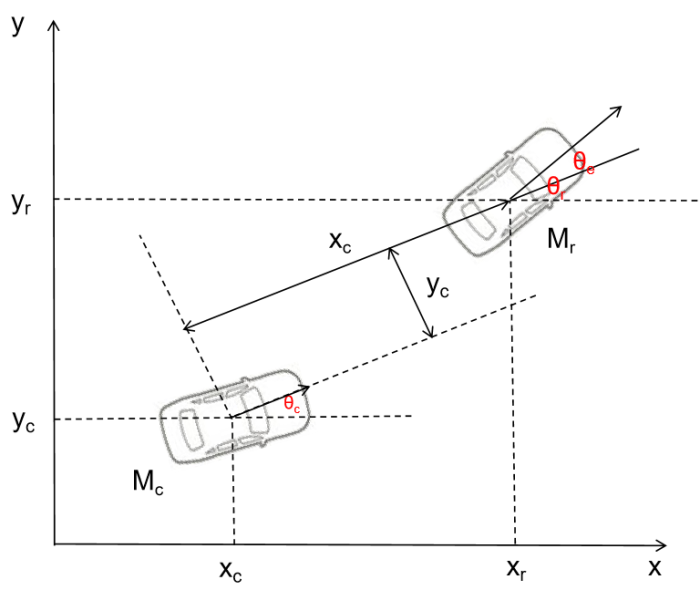
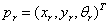 表示自车当前和期望状态下实际纵向位置、横向位置和航向角,而
表示自车当前和期望状态下实际纵向位置、横向位置和航向角,而
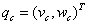 表示是当前速度和横摆角,其中vc和wc分别为车辆当前实际的速度和横摆角速度,在运动学模型中他们是控制输入。
表示是当前速度和横摆角,其中vc和wc分别为车辆当前实际的速度和横摆角速度,在运动学模型中他们是控制输入。
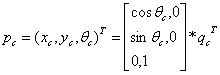
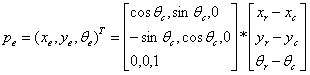
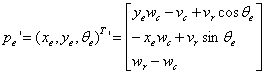
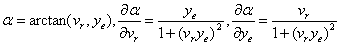
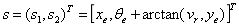
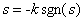
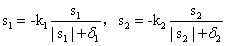
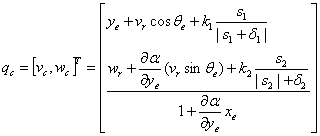
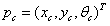 ;
;
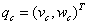 ;
;















获取更多评论