本文在二维极坐标下建立了在定子齿上开辅助槽的表贴式永磁电机空载时的磁场解析模型。如图1所示,电机被分为5个求解子域:子域Ⅰ(永磁体),子域Ⅱ(气隙),子域Ⅲ(电枢槽),子域Ⅳ(电枢槽开口),子域Ⅴ(辅助槽)。以矢量磁位为位函数,在各个子域建立拉普拉斯方程或泊松方程,推导了电机空载时相关性能参数的计算公式。然后,以一台32极48槽的电动车用表贴式外转子轮毂永磁电机为例,通过有限元法和齿槽转矩实验对该解析模型的有效性和精确性进行了验证,并基于该解析模型对影响该轮毂电机齿槽转矩的相关参数进行了优化,削弱了齿槽转矩。

本文以外转子表贴式永磁电机进行模型推导和计算,该模型也同样适用于内转子永磁电机。图1所示为表贴式永磁电机的1/4截面示意图。为了便于分析,需做以下假设:

(1)定、转子铁芯材料的磁导率无穷大;

(2)在二维平面内,忽略电机的端部效应;

(3)永磁体的退磁特性为线性;

(4)定子槽、槽开口、辅助槽均为形状规则的径向扇形结构,如图1所示;

(5)假定永磁体之间间隙的相对磁导率与永磁体的相同,永磁体的相对磁导率μr≠1。

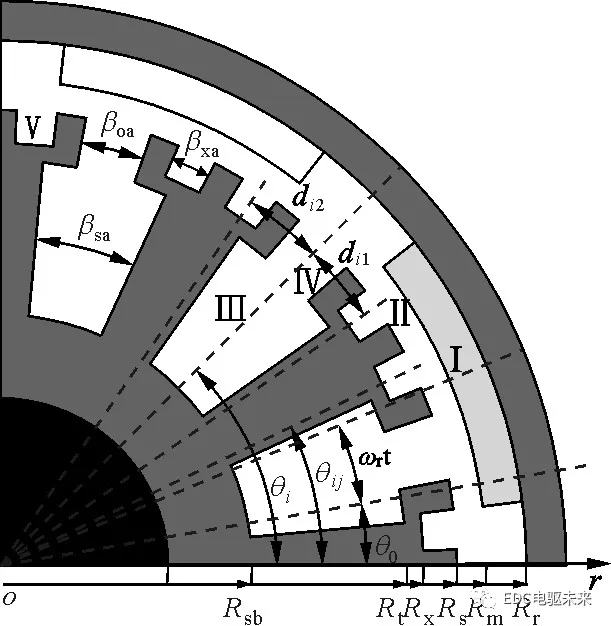
图1 永磁电机各子域的符号和定义

在图1中:将二维极坐标系(r,θ)固定在定子上,且规定齿的中心线位置为θ=0°;θ0为转子在最初位置时磁极的N极中心线与定子(θ=0°)的夹角;ωr为转子的旋转角速度;βsa为电枢槽宽角;βoa为电枢槽开口宽角;βxa为辅助槽宽角;dij为第i个槽两侧的第j个辅助槽中心线距槽中心位置的宽度角;θi为第i个槽和槽开口的中心位置:θi=2π/Ns(i-1/2),其中Ns为电机槽数;θij为第i个电枢槽对应的第j个辅助槽的中心位置,θij=θi+dij。

磁场与矢量磁位的关系为

2A=-×B

(1)

在二维平行平面场中,矢量磁位A仅有z方向分量,故有

Azy=Azyez

(2)

可得各子域的矢量磁位方程为

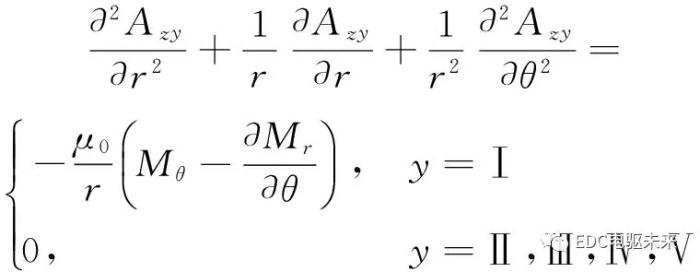
(3)

式中:Azy为矢量磁位,下角标y代表不同子域。

在永磁体区域中,剩余磁化强度M可表示为

M=Mrr+Mθθ

(4)

式中:Mr和Mθ是永磁体剩余磁化强度的径向和切向分量[15]。

由于转子铁芯的磁导率为无穷大,故沿着转子轭(r=Rr)边界满足条件

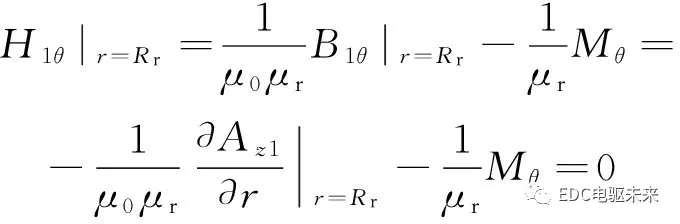
(5)

通过分离变量法,利用以上边界条件求得永磁体子域的矢量磁位表达式为

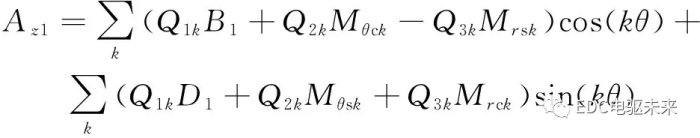
(6)

式中

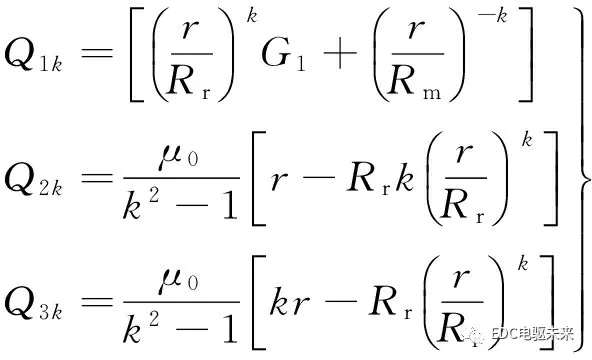
(7)

Mθck、Mθsk、Mrck、Mrsk可参见文献[15];B1、D1是需要求解的谐波系数;k为谐波阶次。

通过分离变量法,求得气隙子域的矢量磁位

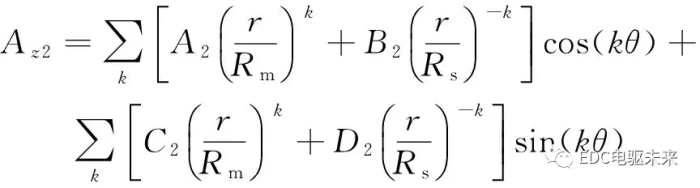
(8)

式中:A2、B2、C2、D2为待求解的气隙子域的谐波系数。

由于铁芯磁导率为无穷大,所以电枢槽子域的2个边界和处的边界条件为

(9)

沿着电枢槽底部的边界满足

(10)

根据分离变量法以及式(9)和式(10)的边界条件,可求得第i个槽子域的矢量磁位表达式为

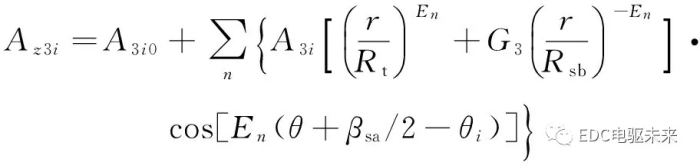
(11)

式中

(12)

A3i0、A3i是待求解的谐波系数;n为谐波阶次。

槽开口子域2个边界和处的边界条件为

(13)

通过分离变量法解得第i个槽开口子域的矢量磁位通解为

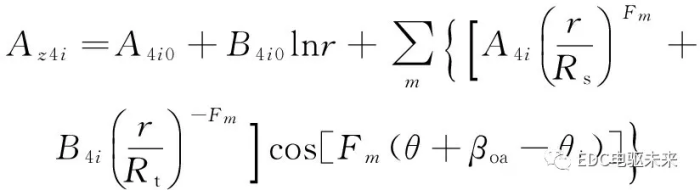
(14)

式中

Fm=mπ/βoa

(15)

A4i0、B4i0、A4i和B4i是待求解的谐波系数;m为谐波阶次。

辅助槽子域的2个边界和处的边界条件为

(16)

沿着槽底部的边界满足

(17)

根据分离变量法以及式(16)和式(17)的边界条件,可求得第(i-1)Nx+j个辅助槽子域的矢量磁位通解为

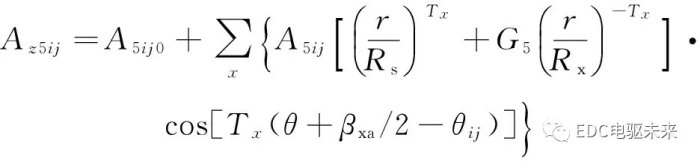
(18)

式中

(19)

A5ij0、A5ij是待求谐波系数;Nx为每齿上的辅助槽数;x为谐波阶次。

根据径向磁通密度连续性和切向磁场强度连续性,可得各子域之间的分界面条件,进而求解谐波系数。矢量磁位与磁通密度的关系为

(20)

永磁体子域和气隙子域分界面(r=Rm)的条件为

Az1|r=Rm=Az2|r=Rm

(21)

H1θ|r=Rm=H2θ|r=Rm

(22)

根据子域1、2中磁通密度B与磁场强度H的关系,式(22)可变换为

(23)

2.2 电枢槽开口子域和气隙子域的分界面(r=Rs)

由于定子铁芯的磁导率为无穷大,所以沿着电枢槽开口子域和气隙子域的分界面(r=Rs),在[0,2π]整个圆周的切向磁通密度分布函数为

(24)

故该分界面的条件为

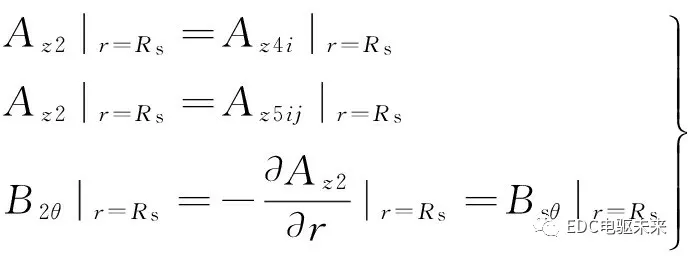
(25)

2.3 电枢槽子域和电枢槽开口子域分界面(r=Rt)

沿着电枢槽子域和电枢槽开口子域分界面(r=Rt),在电枢槽子域范围(θi-βsa/2≤θ≤θi+βsa/2)的切向磁通密度分布函数为

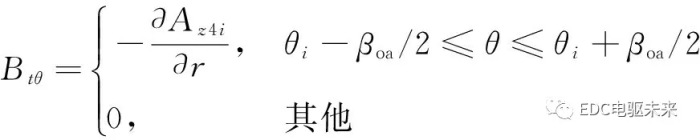
(26)

故该分界面的条件为

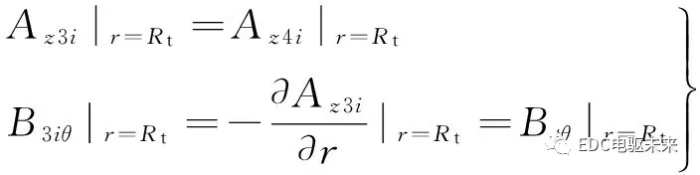
(27)

将以上得到的各子域之间的分界面条件作傅里叶级数展开(见附录A),并联立方程组,可求得前述各个子域的谐波系数。

以一台32极48槽的电动车用外转子表贴式永磁轮毂电机为研究对象,其参数如下:极数2p=32,槽数Ns=48,槽宽角βsa=3.79°,充磁方式为径向,齿尖边缘高(Rs-Rt)=2 mm,轴向长度la=40 mm,槽底半径Rsb=104.5 mm,额定转速为600 r/min,槽开口底部半径Rt=140.3 mm,永磁体厚度为6.3 mm,槽开口顶部半径Rs=142.3 mm,磁通密度Br=1.2 T,永磁体表面半径Rm=143.5 mm,永磁体磁导率μr=1.05,转子轭内表面半径Rr=149.8 mm,槽开口宽度角βoa=1.39°,极弧系数αp=0.7,并联支路数为16,初始位置角θ0=5.625°,节距为1,每相匝数为523,额定功率为10 kW,额定转矩为160 N·m。在MATLAB软件中进行编程求解析解时,谐波阶次分别取:k=400,m=5,n=10,x=5(开辅助槽时)。

根据式(20)可求得径向磁通密度

sin(kθ)+

(28)

切向磁通密度

(29)

将通过分界面条件求解得到的气隙子域的谐波系数A2、B2、C2、D2代入式(28)和(29),得

(30)

(31)

式中:χrsk、χrck、χαsk、χαck是半径为r的圆周上气隙磁通密度径向和切向分量的各次谐波幅值。

图2为电机空载时气隙中心位置r=(Rm+Rs)/2处的径向、切向磁通密度的解析解与有限元解,从中可以看出,解析解与有限元解吻合良好,验证了解析模型的有效性和精确性。

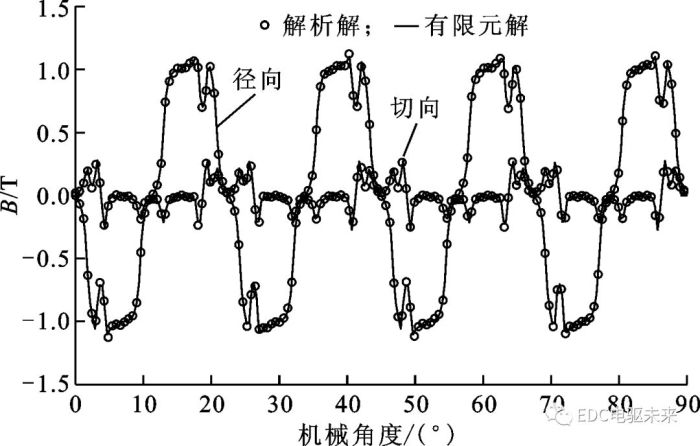
图2 磁通密度有限元解和解析解的对比

假设电枢槽中的绕组均匀分布,由于每个槽中左、右放置了2个线圈边,则2个线圈边的磁链计算公式为

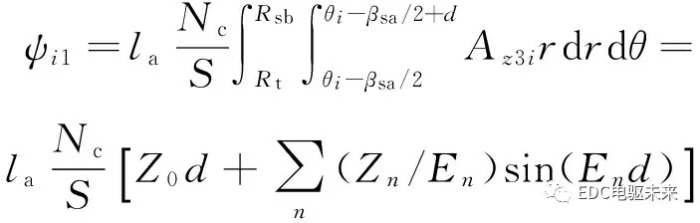
(32)

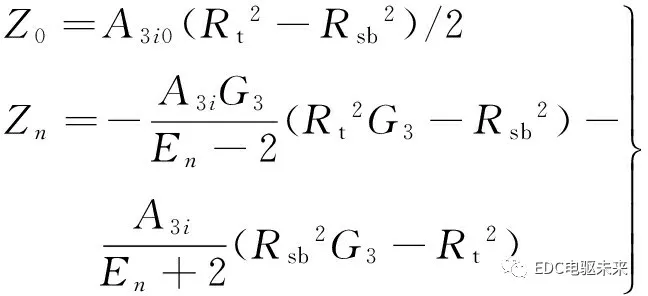
(33)

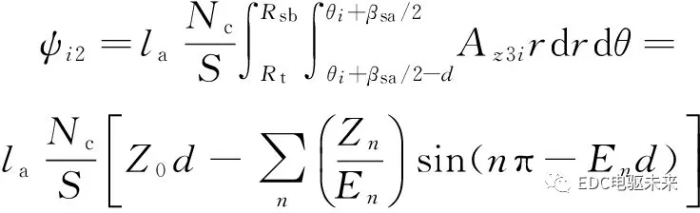
(34)

(35)

式中:Nc为线圈的匝数;S为电枢槽内一个线圈边的面积;d为每个线圈边所占的周向弧度。

三相绕组线圈在槽中的分布可定义为矩阵

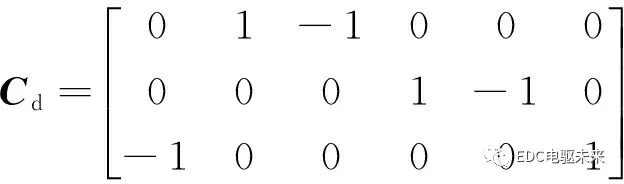
(36)

(37)

式中:C为电机的绕组分布矩阵;w为单元电机数。

所以,每相的总磁链为

(38)

反电势为

(39)

图3和图4分别为电机在额定转速为600 r/min时C相的空载磁链和空载反电动势变化,解析解与有限元解同样吻合得较好,进一步证明了本文解析模型的有效性和精确性。

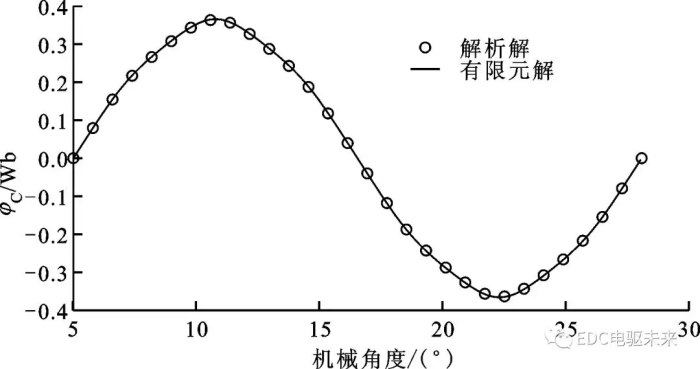
图3 电机转速为600 r/min时的空载C相磁链变化

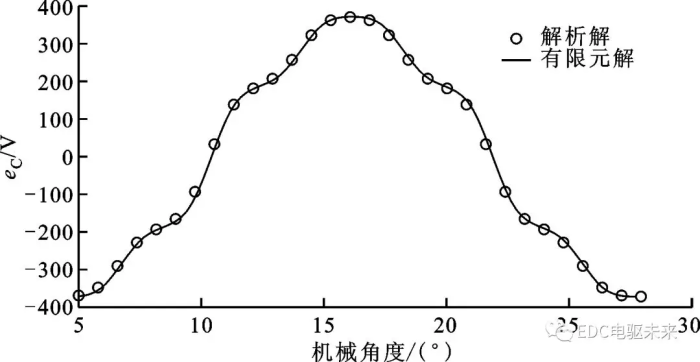
图4 电机转速为600 r/min时的空载C相反电动势变化

齿槽转矩由永磁体和电枢铁芯之间的相互作用产生。采用麦克斯韦张量法计算齿槽转矩,取气隙子域中心位置处的圆周为积分路径

(40)

齿槽转矩表达式为

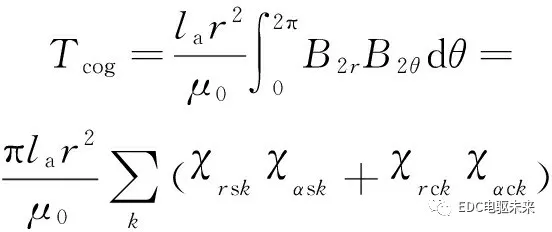
(41)

式中:la为电机的轴向长度。

由式(41)可知:精确的气隙磁通密度是精确计算齿槽转矩的关键;只有气隙磁通密度的径向和切向分量中的同阶次的谐波相互作用才能产生齿槽转矩。

图5所示为齿槽转矩在1个周期内的解析解、有限元解及实验结果的对比,可见三者的吻合程度较高,再次证明了解析模型的有效性和精确性。图5中的齿槽转矩实验值是在测试系统将转速控制为2 r/min时,由扭矩转速测量仪测得的。

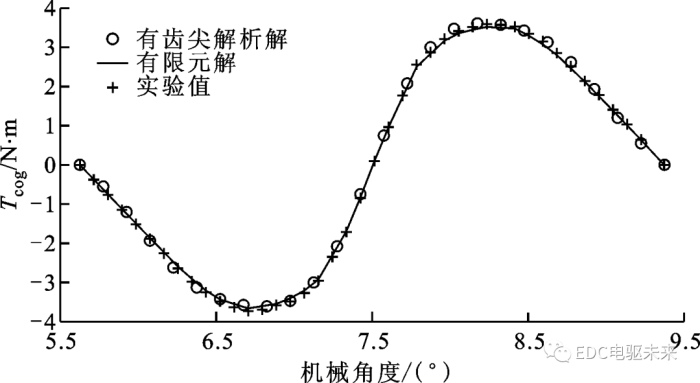
图5 电机转速为2 r/min时的齿槽转矩

前面计算了永磁电机的空载性能,证明本文的解析模型有效且精度较高。因此,下面基于该解析模型对电机的齿槽转矩进行优化。

研究发现,定子齿上开1、3、4或5个辅助槽均不能降低齿槽转矩,只有开2个辅助槽时能够削弱齿槽转矩。本文的解析模型也可用于研究设置任意位置和数量的辅助槽。图6所示为在定子齿上均匀对称开有2个辅助槽(即dij=±2.82°)时,齿槽转矩峰值随辅助槽宽度和深度的变化。从图中可以看出,齿槽转矩峰值几乎不随辅助槽深度而变化,当辅助槽宽度与电枢槽开口宽度的比值为0.6时齿槽转矩最小,为3.025 N·m,相比不开辅助槽时的齿槽转矩峰值3.6 N·m减小了16.6%。

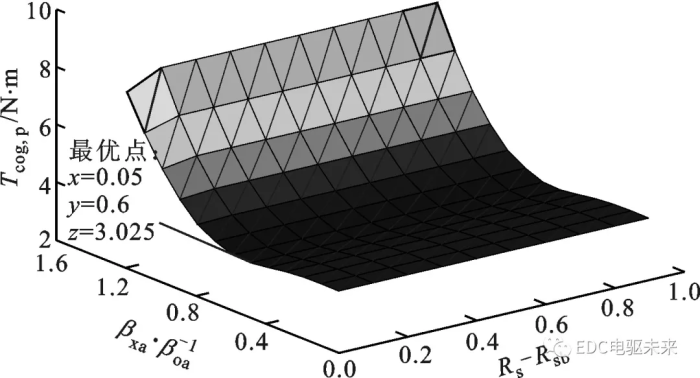
图6 解析预测的辅助槽宽和槽深对齿槽转矩峰值的影响

图7所示为不开辅助槽时齿槽转矩峰值随极弧系数和电枢槽开口宽度的变化,从中可以清晰地看出:当极弧系数确定时,齿槽转矩峰值基本上都是随着电枢槽开口宽度的增加而变大,只有当极弧系数为0.75时,趋势才是相反的;当极弧系数为0.7、电枢槽开口宽度为0.02 rad时,齿槽转矩最小,为2.851 N·m。

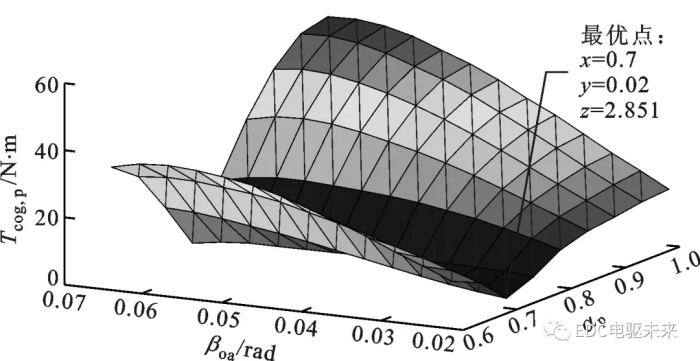
图7 解析预测的极弧系数和电枢槽开口宽度对齿槽转矩峰值的影响

根据以上利用解析模型得到的电机各参数的最优值进行解析计算,并利用有限元法进行验证。

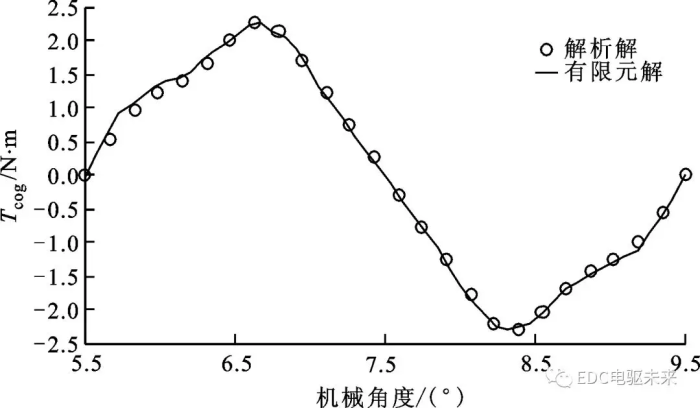
图8 电机转速为2 r/min时的齿槽转矩

图8为优化后的齿槽转矩,从中可以看出,优化后的齿槽转矩峰值为2.26 N·m,相比优化前的3.6 N·m降低了37.2%。图9为优化后的开有2个辅助槽时的气隙磁通密度分布,与图2相比,辅助槽尺寸、极弧系数和槽开口宽度的改变对磁通密度的影响并不大,但是可以有效削弱齿槽转矩,说明基于本文解析模型的永磁电机齿槽转矩优化合理有效。由图8和图9可知,解析解与有限元解高度吻合,证明本文提出的带辅助槽永磁电机解析模型是精确和有效的。

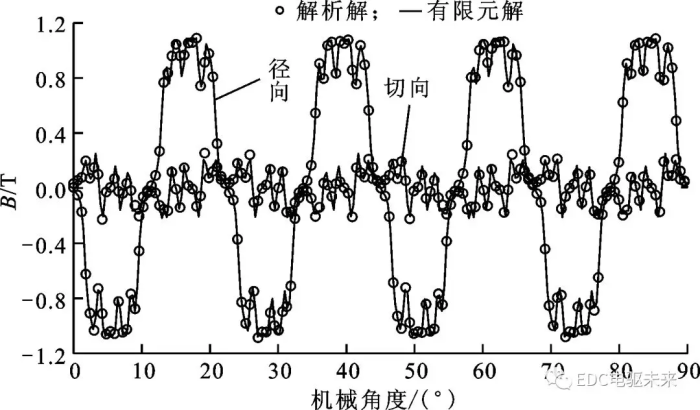
图9 有限元法和解析法预测的气隙磁通密度波形

本文在二维极坐标下建立了一个定子齿上开有辅助槽的表贴式永磁电机的解析模型,考虑了电机的不同充磁方式、不同极槽配合和内、外转子结构;以一台表贴式外转子轮毂永磁电机为研究对象,计算了该电机的空载气隙磁通密度分布、齿槽转矩、磁链和反电动势,并通过有限元法和齿槽转矩实验验证了该解析模型的有效性和精确性;基于解析模型对影响该电机齿槽转矩的相关参数进行了研究和优化。最后,以优化后的参数对该电机的空载气隙磁通密度和齿槽转矩进行了解析计算和有限元计算,两者的计算结果高度吻合,而且有效削弱了齿槽转矩,进一步证明了本文所建立的解析模型的精确性和有效性。该模型不仅计算快、精度高,而且便于通过改变参数来研究电机的性能,有望为表贴式永磁电机的优化与设计提供一种便捷的工具。