模态分析技术是用于对零部件或工程结构系统进行动力学分析的现代化方法和手段，借此可以解决很多工程实际问题。对零部件进行模态分析有利于优化运动机械的整体性能。以汽车制动盘为例，制动盘的模态决定着车辆在制动过程中的部分振动、噪声性能，并对制动盘的寿命、异常磨损等产生影响，测量并确定制动盘的模态频率与振型是研究并解决车辆制动引起振动与噪声的重要手段。

本文利用LMS公司有关模态测试软件对我公司某车型前制动盘进行比较完整的模态测量后，得出了制动盘的各种模态特性；并利用测试软件对测试方法进行了简短的分析，给出了在仅仅想得到零部件固有频率的试验要求下可以简化几何模型、减少测量次数，从而达到最快得到试件固有频率的目的。

制动盘模态特性及要求

作为高速旋转部件，制动盘具有中心对称特性。对于制动盘制动摩擦面，其振型主要是沿圆周均匀分布的变形（对于矩坐标系，相同θ角的各点位相相同，沿圆周呈波浪分布）及相同r（在矩坐标系中）具有相同形变（幅值与位相均相同）的变形。当与制动系统中其他部件组合后，如果某种激励正好位于某一固有频率下，模态被激发，处于共振情形中的这种自身变形会产生强烈的振动与噪音。前一种模态发生共振的可能性更大。通常，制动盘处于本文后面所提到的0/4模态占优势，在产品设计与开发阶段要特别注意此类模态的特性。

测量与分析

利用LMS TestLab 中的MODAL IMPACT模块可对制动盘进行模态测量。用弹性绳把制动盘悬挂起来，将由试件与软绳所组成的系统振动的固有频率控制在5Hz以下，就能完全满足测试要求。

制动盘具有中心对称轴，以中心轴为Z轴，建立柱坐标系。显然，制动盘除Z轴外的其他两方向的刚度比Z轴方向的刚度要大得多，在常规频段振动主要是沿着Z轴方向发生，因此只测定Z轴方向的加速度值即可。制动盘结构相对较小，质量不大，因此在粘贴传感器时应尽量减小附加质量的影响，为此采用分别在多点激励、测取某一点处的响应的方法进行。激励与响应均只有沿Z轴方向的数值。制动盘为小质量、高硬度的部件，固有频率较高，利用LMS Modal Impact模块进行测量。综合考虑传感器频响特性、试件模态特性及测试状况，频率范围选为0～6 400Hz可以满足实际要求。频率的分辨率选为1Hz以下。

1. 精细测量

为了不遗漏每一个模态（包括制动盘固定面的局部，即凸台部分的模态），我们建立了比较精细的几何模型（如图1），摩擦面外、内圈分别设定了24个点，固定凸台上外圈24点、内圈12点，共84点。单向加速度传感器粘贴于摩擦面外圈某点处，分别在每一点沿Z向用力锤进行激励，每一次激励重复3次测量。用PolyMax对测试数据进行处理，所得到的稳态图（所有点响应的总和）如图2。

图1   制动盘的几何模型

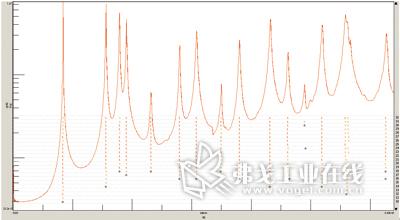
图2   精细测量时利用LMS软件所获得的稳态图

从图1可看出，LMS软件处理的结果非常清晰，通过选取稳态图上标明有s的点很容易把某一固有频率确立下来。从稳态图上可以而且只能确立14个固有频率（模态）。利用软件进一步处理，得到6400Hz以下所有模态的振型（如图3）。

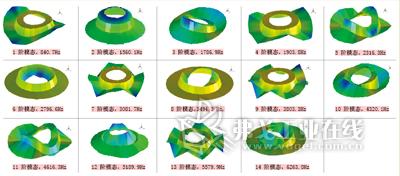
图3   精细测量时利用LMS软件所获得的各模态振型

下面对各级模态做简单分析，首先根据模态的振型对模态进行分类：

（1）按变形部位，可以分为制动摩擦面（如图3中的1、4、7、10、13等）、固定凸台（如图3中的6、8、14等）及其摩擦面与凸台组合的变形。随着制动盘的磨损，与摩擦面有关的模态固有频率将发生改变。

（2）按变形形态分类，可以分为沿周边波浪式的变形（在矩坐标系中摩擦面相同θ角的各点变形位相相同），如图3中的1、4、7、10、13等。相同r具有相同变形（位相与幅度）的圆变形，如图3中的2、6、12等。此外，还包含其他组合变形。

可以测出的模态与仪器的精度有关。一般盘式制动系统采用浮动制动钳，凸台部分固定于轮毂上，其模态对系统的影响不是最主要的。制动时，摩擦面部分的模态的激发是产生噪声的主要原因。为此，我们特定义图3中的第1、4、7、10、13阶模态分别为0/2、0/3、0/4、0/5、0/6，而将圆变形，如图3中的第2、12阶模态，定义为1/1、1/2。其他还有较为复杂的组合振型或仅仅凸台上各种振型。

2. 简易测量

制动盘质量较小，任何外在的附加质量对测量结果都将产生影响，在上面的测量过程中，我们利用一只单向传感器对所有点进行激励来测试，得到了较好的效果。在后面的分析中会发现，欲测试出尽量高阶的模态需要进行大量几何点的测试。实际工作中，在产品开发的某几个阶段以及在正式生产中每一次的测试经常需要大量的被测试件，这些都带来较大的工作量。为此，我们又进一步探索利用LMS相关软件进行简易测试方法，以期能达到模态测试的目的，且减少工作量。

首先，建立简单的几何模型，重点关注制动盘的摩擦面，该平面模型仅包括8点，连接成中间有一方孔的正方形。与精细测量的过程完全相同，分别对几何模型中的每一点进行激励，测取相关数据，由此所得到的稳态图如图4所示。图中曲线的形状及具有稳定的模态的频率位置与精细测量所得到的稳态图（图2）基本一致。除了精细测量中的第8阶模态（3494.3Hz），其他模态的位置在要求的精度内完全相同。从图3的模态振型中可以发现，此模态完全是凸台的变形，与摩擦面无关。其他结果参数的比较如表1所示。

表1   不同几何模型或测试点的数量0/4模态各参数比较

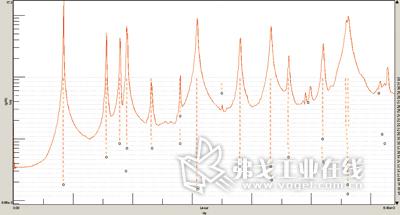
图4   建立简单几何模型，利用PolyMax所获得的稳态图

3. 少点测量

为进一步简化测试过程，我们在试验过程中尝试仅对部分几何模型中的点进行激励，探讨测量结果的可靠性。

试验过程中，我们利用“简易测量”中的8点简单几何模型，仅对其中的部分点进行激励，其他测试及求算过程不变，得到一个稳态图（如图5）。图5的稳态图与图4几乎没有差别，模态数量完全一样，各模态的频率在测量精度内也完全相等。

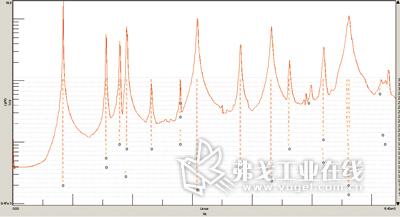
图5   建立简单几何模型，通过部分几何点的测试，利用PolyMax所获得的稳态图

4. 结果比较

以上3种方法所建立的几何模型差别较大，测试的轮次也各不相同，但数据结果均能满足实际要求。以我们最为关注的制动盘0/4模态为例，各模态参数比较结果如表1。从表1可看出，通过简单的几何模型和少量的测量轮次即可得到试件的模态参量，包括固有频率、阻尼比、模态刚度、模态质量等，并且在要求的精度内完全相等。当然，模态振型的得出还是需要充分多点的几何模型，并且要进行充分多的点的激励和测量。

下面简单分析欲判别出模态振型建立几何模型所需要的点的数量。以摩擦面的模态为例，主要是沿周边的波浪式的变形。一个波浪需要5点来描述其变形，考虑到所有波浪形成一圆圈，平均一个波浪4点。如果需要描绘出沿制动摩擦面周边的波浪变形，各级模态在制动盘的边缘所需要的几何点的数量如表2。其他部位几何模型点的数量的要求将根据边缘部位点的数量作相应的确定。

表2   波浪变形模态几何模型测点数量

结语

利用LMS TestLab模态测试软件，通过对某制动盘模态的测量与分析，可以得出以下结论：

1. 利用LMSTestLab中的Modal Impact软件工具，能很好地得出制动盘6 400Hz以下所有的模态，包含凸台的局部模态。包含摩擦面与凸台的模态较为复杂，有的是摩擦面的模态，有的是凸台的模态，但大部分是它们的组合。

2. 建立最简单的几何模型，只进行部分几何点的测试也能得到绝大部分的模态及其各种参数；但如果要判别出具体的模态振型还是要根据所要判别的具体模态的振型状况建立包含充分多的点的几何模型，并且对各点进行激励、测试。